
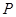 是双曲线
是双曲线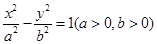 与圆
与圆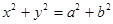 在第一象限的交点,其中
在第一象限的交点,其中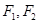 分别是双曲线的左、右焦点,且
分别是双曲线的左、右焦点,且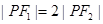 ,则双曲线的离心率为
,则双曲线的离心率为A.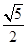 | B.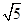 | C. | D. |
 -
-  =1(a>,b>0)与圆x2+y2=a2+b2在第一象限的交点,推导出∠F1PF2=90°.再由|PF1|=2|PF2|,知|PF1|=4a,|PF2|=2a,由此求出c=
=1(a>,b>0)与圆x2+y2=a2+b2在第一象限的交点,推导出∠F1PF2=90°.再由|PF1|=2|PF2|,知|PF1|=4a,|PF2|=2a,由此求出c= 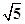 a,从而得到双曲线的离心率.
a,从而得到双曲线的离心率. -
- =1(a>,b>0)与圆x2+y2=a2+b2在第一象限的交点,
=1(a>,b>0)与圆x2+y2=a2+b2在第一象限的交点, =c,
=c,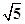 a,
a, =
=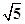 .
.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com