
【题目】如图,![]() ,
,![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() 的左、右焦点,直线
的左、右焦点,直线![]() ,将线段
,将线段![]() ,
,![]() 分成两段,其长度之比为
分成两段,其长度之比为![]() ,设
,设![]() 是
是![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.

(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2) ![]()
【解析】
(1)设![]() ,由线段长度之比可列出等式求出c,代入离心率公式求得a,再求出b,即可求得椭圆的标准方程;(2)当直线AB斜率不存在时,直线AB的方程为
,由线段长度之比可列出等式求出c,代入离心率公式求得a,再求出b,即可求得椭圆的标准方程;(2)当直线AB斜率不存在时,直线AB的方程为![]() ,求出P、Q坐标直接求
,求出P、Q坐标直接求![]() ;当直线AB斜率存在时,直线方程与椭圆方程联立可得关于x的一元二次方程,利用韦达定理求出
;当直线AB斜率存在时,直线方程与椭圆方程联立可得关于x的一元二次方程,利用韦达定理求出![]() 、
、![]() ,可求得
,可求得![]() 的关于m的表达式,根据题意求出m的范围即可求得
的关于m的表达式,根据题意求出m的范围即可求得![]() 的范围.
的范围.
(1)设![]() ,因为直线
,因为直线![]() ,将线段
,将线段![]() ,
,![]() 分成两段,其长度之比为
分成两段,其长度之比为![]() ,
,
所以![]() ,解得
,解得![]() ,
,
又离心率![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以椭圆C的方程为:![]() ;
;
(2)①当直线AB斜率不存在时,直线AB的方程为![]() ,此时PQ与x轴重合,
,此时PQ与x轴重合,
![]() ,因为
,因为![]() ,
,![]() ,
,
所以![]() ;
;
②当直线AB斜率存在时,设直线AB的斜率为k,![]() ,
,![]() ,
,
因为M是线段AB的中点,所以![]() ,
,![]() ,
,
由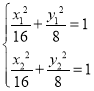 ,整理得
,整理得![]() ,
,
则![]() ,所以
,所以![]() ,此时直线PQ的斜率为
,此时直线PQ的斜率为![]() ,直线PQ的方程为:
,直线PQ的方程为:![]() 即
即![]() ,
,
设![]() ,
,
联立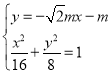 ,消去y,可得
,消去y,可得![]() ,
,
则![]() ,
,
![]() ,
,
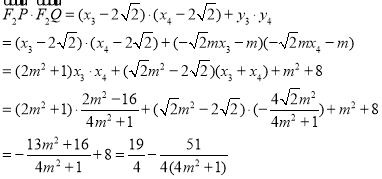
直线![]() 与椭圆
与椭圆![]() 的交点为
的交点为![]() ,
,
因为线段![]() 的中点
的中点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,则
,则![]() ,
,
![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】下列四种说法:
①命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;
”;
②若不等式![]() 的解集为
的解集为![]() ,则不等式
,则不等式![]() 的解集为
的解集为![]() ;
;
③对于![]() ,
,![]() 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是![]() ;
;
④已知p:![]() ,q:
,q:![]() (
(![]() ),若p是q的充分不必要条件,则实数a的取值范围是
),若p是q的充分不必要条件,则实数a的取值范围是![]()
正确的有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长度为![]() 的线段
的线段![]() 的两个端点
的两个端点![]() 分别在
分别在![]() 轴和
轴和![]() 轴上运动,动点
轴上运动,动点![]() 满足
满足![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() ,且斜率不为零的直线
,且斜率不为零的直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,在
,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 的斜率之积为常数?若存在,求出定点
的斜率之积为常数?若存在,求出定点![]() 的坐标以及此常数;若不存在,请说明理由.
的坐标以及此常数;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】绿色已成为当今世界主题,绿色动力已成为时代的驱动力,绿色能源是未来新能源行业的主导.某汽车公司顺应时代潮流,最新研发了一款新能源汽车,并在出厂前对100辆汽车进行了单次最大续航里程(理论上是指新能源汽车所装载的燃料或电池所能够提供给车行驶的最远里程)的测试.现对测试数据进行分析,得到如图所示的频率分布直方图.

(1)估计这100辆汽车的单次最大续航里程的平均值![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)根据大量的汽车测试数据,可以认为这款汽车的单次最大续航里程![]() 近似地服从正态分布
近似地服从正态分布![]() ,经计算第(1)问中样本标准差
,经计算第(1)问中样本标准差![]() 的近似值为50.用样本平均数
的近似值为50.用样本平均数![]() 作为
作为![]() 的近似值,用样本标准差
的近似值,用样本标准差![]() 作为
作为![]() 的估计值;
的估计值;
(ⅰ)现从该汽车公司最新研发的新能源汽车中任取一辆汽车,求它的单次最大续航里程恰好在200千米到350千米之间的概率;
(ⅱ)从该汽车公司最新研发的新能源汽车中随机抽取10辆,设这10辆汽车中单次最大续航里程恰好在200千米到350千米之间的数量为![]() ,求
,求![]() ;
;
(3)某汽车销售公司为推广此款新能源汽车,现面向意向客户推出“玩游戏,送大奖”活动,客户可根据抛掷硬币的结果,操控微型遥控车在方格图上行进,若遥控车最终停在“胜利大本营”,则可获得购车优惠券.已知硬币出现正、反面的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第50格.遥控车开始在第0格,客户每掷一次硬币,遥控车向前移动一次,若掷出正面,遥控车向前移动一格(从![]() 到
到![]() ),若掷出反面,遥控车向前移动两格(从
),若掷出反面,遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第
),直到遥控车移到第49格(胜利大本营)或第50格(失败大本营)时,游戏结束.设遥控车移到第![]() 格的概率为
格的概率为![]() ,其中
,其中![]() ,试说明
,试说明![]() 是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
是等比数列,并解释此方案能否成功吸引顾客购买该款新能源汽车.
参考数据:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某鲜花批发店每天早晨以每支2元的价格从鲜切花生产基地购入某种玫瑰,经过保鲜加工后全部装箱(每箱500支,平均每支玫瑰的保鲜加工成本为1元),然后以每箱2000元的价格整箱出售.由于鲜花的保鲜特点,制定了如下促销策略:若每天下午3点以前所购进的玫瑰没有售完,则对未售出的玫瑰以每箱1200元的价格降价处理.根据经验,降价后能够把剩余玫瑰全部处理完毕,且当天不再购进该种玫瑰.因库房限制每天最多加工6箱.
(1)若某天此鲜花批发店购入并加工了6箱该种玫瑰,在下午3点以前售出4箱,且6箱该种玫瑰被6位不同的顾客购买.现从这6位顾客中随机选取2人赠送优惠卡,求恰好一位是以2000元价格购买的顾客且另一位是以1200元价格购买的顾客的概率:
(2)此鲜花批发店统计了100天该种玫瑰在每天下午3点以前的销售量t(单位:箱),统计结果如下表所示(视频率为概率):
t/箱 | 4 | 5 | 6 |
频数 | 30 | x | s |
①估计接下来的一个月(30天)该种玫瑰每天下午3点前的销售量不少于5箱的天数并说明理由;
②记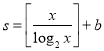 ,
,![]() ,若此批发店每天购进的该种玫瑰箱数为5箱时所获得的平均利润最大,求实数b的最小值(不考虑其他成本,
,若此批发店每天购进的该种玫瑰箱数为5箱时所获得的平均利润最大,求实数b的最小值(不考虑其他成本,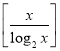 为
为![]() 的整数部分,例如:
的整数部分,例如:![]() ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的上顶点到左焦点
的上顶点到左焦点![]() 的距离为
的距离为![]() .直线
.直线![]() 与椭圆
与椭圆![]() 交于不同两点
交于不同两点![]() 、
、![]() (
(![]() 、
、![]() 都在
都在![]() 轴上方),且
轴上方),且![]() .
.

(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 为椭圆与
为椭圆与![]() 轴正半轴的交点时,求直线
轴正半轴的交点时,求直线![]() 方程;
方程;
(3)对于动直线![]() ,是否存在一个定点,无论
,是否存在一个定点,无论![]() 如何变化,直线
如何变化,直线![]() 总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
总经过此定点?若存在,求出该定点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:①两个随机变量的线性相关性越强,相关系数的绝对值越接近1;②在回归分析中,可用相关指数![]() 的值判断拟合效果,
的值判断拟合效果,![]() 越小,模型的拟合效果越好; ③若数据
越小,模型的拟合效果越好; ③若数据![]() 的方差为1,则
的方差为1,则![]() 的方差为4;④已知一组具有线性相关关系的数据
的方差为4;④已知一组具有线性相关关系的数据![]() ,其线性回归方程
,其线性回归方程![]() ,则“
,则“![]() 满足线性回归方程
满足线性回归方程![]() ”是“
”是“![]() ,
,![]() ”的充要条件;其中真命题的个数为( )
”的充要条件;其中真命题的个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的内接等边三角形
的内接等边三角形![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点).
为坐标原点).
(1)试求抛物线![]() 的方程;
的方程;
(2)已知点![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是以点
是以点![]() 为直角顶点的直角三角形.
为直角顶点的直角三角形.
①求证:直线![]() 恒过定点;
恒过定点;
②过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点
于点![]() ,试求点
,试求点![]() 的轨迹方程,并说明其轨迹是何种曲线.
的轨迹方程,并说明其轨迹是何种曲线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com