
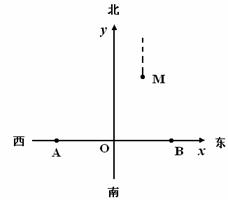
如图,相距200海里的A、B两地分别有救援A船和B船.在接到求救信息后,A船能立即出发,B船因港口原因需2小时后才能出发,两船的航速都是30海里/小时.在同时收到求救信息后,A船早于B船到达的区域称为A区,否则称为B区.若在A地北偏东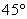 方向,距A地
方向,距A地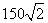 海里处的
海里处的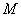 点有一艘遇险船正以10海里/小时的速度向正北方向漂移.
点有一艘遇险船正以10海里/小时的速度向正北方向漂移.
⑴求A区与B区边界线(即A、B两船能同时到达的点的轨迹)方程;
⑵问:
①应派哪艘船前往救援?
②救援船最快需多长时间才能与遇险船相遇?(精确到 小时)
小时)
 备战中考寒假系列答案
备战中考寒假系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com