练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．数列{an}的前n项和是Sn，若数列{an}的各项按如下规则排列：$\frac{1}{2}$，$\frac{1}{3}$，$\frac{2}{3}$，$\frac{1}{4}$，$\frac{2}{4}$，$\frac{3}{4}$，$\frac{1}{5}$，$\frac{2}{5}$，$\frac{3}{5}$，$\frac{4}{5}$，$\frac{1}{6}$，…，若Sk＜10，Sk+1≥10，则ak=$\frac{5}{7}$．

    分析 把原数列分成$\frac{1}{2}$；$\frac{1}{3}$，$\frac{2}{3}$；$\frac{1}{4}$，$\frac{2}{4}$，$\frac{3}{4}$；$\frac{1}{5}$，$\frac{2}{5}$，$\frac{3}{5}$，$\frac{4}{5}$；$\frac{1}{6}$，…，构建新数列bn=n，由此利用Sk＜10，Sk+1≥10，能求出ak．

    解答 解：把原数列分成$\frac{1}{2}$；$\frac{1}{3}$，$\frac{2}{3}$；$\frac{1}{4}$，$\frac{2}{4}$，$\frac{3}{4}$；$\frac{1}{5}$，$\frac{2}{5}$，$\frac{3}{5}$，$\frac{4}{5}$；$\frac{1}{6}$，…，
    发现它们的个数是1，2，3，4，5，…
    构建新数列bn，则bn=n等差数列，记bn的前n项和为Tn，
    由等差数列的前n项和得T5=$\frac{5（1+5）}{2}$=$\frac{15}{2}$，${T}_{6}=\frac{6（1+6）}{2}=\frac{21}{2}$，
    ∵Sk＜10，Sk+1≥10，
    ∴ak定在$\frac{1}{7}，\frac{2}{7}，\frac{3}{7}，\frac{4}{7}，\frac{5}{7}，\frac{6}{7}$之中，
    ∵${T}_{5}+\frac{1}{7}+\frac{2}{7}+\frac{3}{7}+\frac{4}{7}+\frac{5}{7}$=9+$\frac{9}{14}$＜10，
    ${T}_{5}+\frac{1}{7}+\frac{2}{7}+\frac{3}{7}+\frac{4}{7}+\frac{5}{7}+\frac{6}{7}$=10+$\frac{1}{2}$＞10，
    ∴ak=$\frac{5}{7}$．
    故答案为：$\frac{5}{7}$．

    点评 本题考查数列的第k项的求法，是中档题，解题时要认真审题，注意等差数列的性质和归纳整理的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．若xlog52≥-1，则函数f（x）=4x-2x+1-3的最小值为（　　）
    A．-4B．-2C．-1D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．在实数集R中，我们定义的大小关系“＞”为全体实数排了一个“序”．类似实数排序的定义，我们定义“点序”记为“＞”：已知M（x1，y1）和N（x2，y2），M＞N，当且仅当“x1＞x2”或“x1=x2且y1＞y2”．定义两点的“⊕”与“?”运算如下：M⊕N=（x1+x2，y1+y2）    M?N=x1x2+y1y2．则下面四个命题：
    ①已知P（2015，2014）和Q（2014，2015），则P＞Q；
    ②已知P（2015，2014）和Q（x，y），若P＞Q，则x≤2015，且y≤2014；
    ③已知P＞Q，Q＞M，则P＞M；
    ④已知P＞Q，则对任意的点M，都有P⊕M＞Q⊕M；
    ⑤已知P＞Q，则对任意的点M，都有P?M＞Q?M．
    其中真命题的序号为①③④（把真命题的序号全部写出）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．将正整数从1开始依次写下来，直至2015为止，得到一个新的正整数：1234…201320142015．这个正整数是几位数（　　）
    A．3506位数B．4518位数C．6953位数D．7045位数

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．函数f（x）在[a，b]上有定义，若对任意x1，x2∈[a，b]，有$f（\frac{{{x_1}+{x_2}}}{2}）≤\frac{1}{2}[f（{x_1}）+f（{x_2}）]$，则称f（x）在[a，b]上具有性质P．设f（x）在[1，3]上具有性质P，现给出如下命题：
    ①f（x）在[1，3]上的图象是连续不断的；
    ②f（x2）在$[1，\;\sqrt{3}]$上具有性质P；
    ③若f（x）在x=2处取得最大值1，则f（x）=1，x∈[1，3]；
    ④任意x1，x2，x3，x4∈[1，3]，有$f（\frac{{{x_1}+{x_2}+{x_3}+{x_4}}}{4}）≤\frac{1}{4}[f（{x_1}）+f（{x_2}）+f（{x_3}）+f（{x_4}）]$．
    其中真命题的序号是（　　）
    A．①②B．①③C．②④D．③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．如图中的程序框图所描述的算法称为欧几里得辗转相除法．若输入m=459，n=357，则输出m=（　　）
    A．51B．17C．9D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．记集合T={0，1，2，3，4，5，6，7，8，9}，$M=\{\frac{a_1}{10}+\frac{a_2}{{{{10}^2}}}+\frac{a_3}{{{{10}^3}}}+\frac{a_4}{{{{10}^4}}}|{a_i}∈T，i=1，2，3，4\}$，将M中的元素按从大到小排列，则第2012个数是（　　）
    A．$\frac{5}{10}+\frac{5}{{{{10}^2}}}+\frac{7}{{{{10}^3}}}+\frac{3}{{{{10}^4}}}$B．$\frac{5}{10}+\frac{5}{{{{10}^2}}}+\frac{7}{{{{10}^3}}}+\frac{2}{{{{10}^4}}}$
    C．$\frac{7}{10}+\frac{9}{{{{10}^2}}}+\frac{8}{{{{10}^3}}}+\frac{8}{{{{10}^4}}}$D．$\frac{7}{10}+\frac{9}{{{{10}^2}}}+\frac{9}{{{{10}^3}}}+\frac{1}{{{{10}^4}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

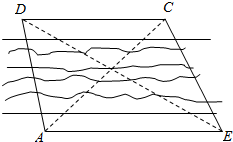    2．为了测量河对岸两个建筑物C、D之间的距离，在河岸边取点A、B，∠BAC=45°，∠DAC=75°，∠ABD=30°，∠DBC=45°，AB=$\sqrt{3}$千米，A、B、C、D在同一个平面内，试求C、D之间的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．如图，△ABC是直角三角形，∠C为直角，D是斜边AB上一点，以BD为直径的圆O与AC相切于点E，与BC相交于点F．
    （1）求证：BE2=BC•BD；
    （2）若DE=6，CF=4，求AE的长．

    查看答案和解析>>

    同步练习册答案