
| A. | 2 | B. | 1 | C. | 4 | D. | 6 |
分析 求出圆F的半径|FA|=$\sqrt{2}$p,A到l的距离,利用△ABD的面积为4$\sqrt{2}$,求出p的值.
解答 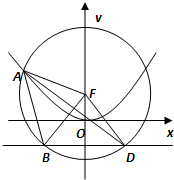 解:由已知可得△BFD为等腰直角三角形,|BD|=2p,
解:由已知可得△BFD为等腰直角三角形,|BD|=2p,
圆F的半径|FA|=$\sqrt{2}$p.
由抛物线定义可知A到l的距离d=|FA|=$\sqrt{2}$p.
因为△ABD的面积为4$\sqrt{2}$,所以$\frac{1}{2}$|BD|•d=4$\sqrt{2}$,即$\frac{1}{2}$•2p•$\sqrt{2}$p=4$\sqrt{2}$,
解得p=-2(舍去),p=2.
故选:A.
点评 本题考查抛物线的定义,考查三角形面积的计算,考查学生的计算能力,属于中档题.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
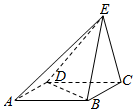 如图ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.
如图ABCD是平行四边形,已知AB=2BC=4,BD=2$\sqrt{3}$,BE=CE,平面BCE⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | B. | $\frac{{x}^{2}}{8}$-$\frac{{y}^{2}}{6}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{6}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{6}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
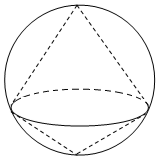 一个透明的球形装饰品内放置了两个公共底面的圆锥如图,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的$\frac{3}{16}$,则较大圆锥与较小圆锥的体积之比为3:1.
一个透明的球形装饰品内放置了两个公共底面的圆锥如图,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球面面积的$\frac{3}{16}$,则较大圆锥与较小圆锥的体积之比为3:1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
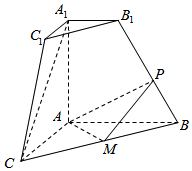 如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2.直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.M为线段BC的中点,P为线段BB1上的动点.
如图,在直角梯形AA1B1B中,∠A1AB=90°,A1B1∥AB,AB=AA1=2A1B1=2.直角梯形AA1C1C通过直角梯形AA1B1B以直线AA1为轴旋转得到,且使得平面AA1C1C⊥平面AA1B1B.M为线段BC的中点,P为线段BB1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com