
分析 根据互为反函数的两个函数图象关于y=x对称,可判断①;根据对数式的真数必大于0,可判断②;根据奇函数的定义,可判断③.
解答 解:①函数y=2x与函数y=log2x互为反函数,图象关于y=x对称,故错误;
②当x=-1时,2x+1<0,故方程log5(2x+1)=log5(x2-2)的解集为{3},故错误;
③函数f(x)=ln(1+x)-ln(1-x)的定义域(-1,1)关于原点对称,
且f(-x)=ln(1-x)-ln(1+x)=-f(x),故函数为奇函数,故正确;
故正确的结论是:③,
故答案为:③
点评 本题以命题的真假判断与应用为载体,考查了反函数,对数函数,函数的奇偶性,是函数图象和性质的综合应用,难度中档.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
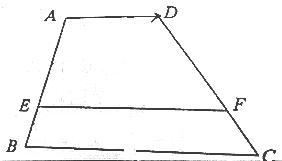 如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.
如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | -1 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 10 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com