
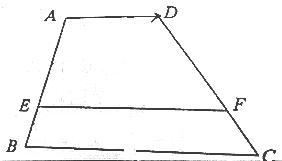
 如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.
如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$. 分析 可延长BA,设交CD的延长线于P,可设BE=a,PA=b,根据条件及相似三角形的比例关系便可得到$\frac{b}{3a+b}=\frac{2}{5}$,可得出b=2a,从而可得到EF=2AD,根据数乘的几何意义便可用$\overrightarrow{a}$表示出$\overrightarrow{EF},\overrightarrow{CB}$.
解答 解:如图,分别延长BA,CD,交于P,设BE=a,PA=b;
设BE=a,PA=b,则AE=2a;
∵AD∥BC,且AD=2,BC=5;
∴$\frac{b}{3a+b}=\frac{2}{5}$;
∴6a+2b=5b;
∴b=2a;
∴EF=2AD;
$\overrightarrow{AD},\overrightarrow{EF},\overrightarrow{CB}$三向量共线,$\overrightarrow{AD}=\overrightarrow{a}$;
∴$\overrightarrow{EF}=2\overrightarrow{a}$,$\overrightarrow{CB}=-\frac{5}{2}\overrightarrow{a}$.
点评 考查相似三角形的比例关系,共线向量基本定理,以及向量数乘的几何意义,注意向量的方向.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com