
分析 ①直接利用对数的运算性质化简求值;②利用对数的换底公式化简;③利用对数的差等于商的对数,对数的和等于乘积的对数化简求值;④利用对数的和等于乘积的对数结合平方差公式运算.
解答 解:①4lg2+3lg5-lg$\frac{1}{5}$=4lg2+3lg5-(lg1-lg5)=4(lg2+lg5)=4;
②$\frac{lo{g}_{5}\sqrt{2}•lo{g}_{49}81}{lo{g}_{25}\frac{1}{3}•lo{g}_{7}\root{3}{4}}$=$\frac{\frac{\frac{1}{2}lg2}{lg5}•\frac{4lg3}{2lg7}}{\frac{-lg3}{2lg5}•\frac{\frac{2}{3}lg2}{lg7}}$=$\frac{1}{-\frac{1}{3}}=-3$;
③2log32-log3$\frac{32}{9}$+log38-5${\;}^{lo{g}_{5}3}$=$lo{g}_{3}4-lo{g}_{3}\frac{32}{9}+lo{g}_{3}8-3$=$lo{g}_{3}\frac{36}{32}+lo{g}_{3}8-3$=log39-3=-1;
④log2$\sqrt{8+4\sqrt{3}}$+log2$\sqrt{8-4\sqrt{3}}$=$lo{g}_{2}\sqrt{64-48}$=$lo{g}_{2}\sqrt{16}=lo{{g}_{2}}^{4}=2$.
点评 本题考查对数的运算性质,考查计算能力,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
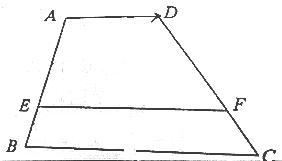 如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.
如图,已知:梯形ABCD中,AD∥EF∥BC,AE=2BE,AD=2,BC=5,设$\overrightarrow{AD}$=$\overrightarrow{a}$,用$\overrightarrow{a}$表示$\overrightarrow{EF}$,$\overrightarrow{CB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -3 | C. | -1 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com