
 вбжЊКЏЪ§fЃЈxЃЉЕФЖЈвхгђЮЊ[-1ЃЌ5]ЃЌВПЗжЖдгІжЕШчЯТБэЃЌ
вбжЊКЏЪ§fЃЈxЃЉЕФЖЈвхгђЮЊ[-1ЃЌ5]ЃЌВПЗжЖдгІжЕШчЯТБэЃЌ| x | -1 | 0 | 4 | 5 |
| fЃЈxЃЉ | 1 | 2 | 2 | 1 |
| AЁЂЂйЂк | BЁЂЂлЂм |
| CЁЂЂйЂкЂм | DЁЂЂкЂлЂм |



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| y2 |
| b2 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| Іа |
| 3 |
| 5Іа |
| 12 |
| 11Іа |
| 12 |
| Іа |
| 3 |
| Іа |
| 2 |
| 5Іа |
| 8 |
| Іа |
| 3 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
| lim |
| nЁњЁо |
| 22 |
| a2 |
| 23 |
| a3 |
| 2n |
| an |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
|
| AЁЂгазюаЁжЕ1 | ||||
BЁЂгазюаЁжЕ
| ||||
CЁЂгазюДѓжЕ
| ||||
DЁЂгазюаЁжЕ
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
AЁЂ
| ||
BЁЂ
| ||
CЁЂ
| ||
DЁЂ
|
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
|
| AЁЂ-1 | BЁЂ0 | CЁЂ4 | DЁЂ5 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
AЁЂвбжЊcosІС=
| |||||||||||
| BЁЂвбжЊ2a=3b=kЃЈkЁй1ЃЉЧв2a+b=abЃЌдђЪЕЪ§kЕФжЕЮЊ36 | |||||||||||
CЁЂвбжЊКЏЪ§f(x)=
| |||||||||||
| DЁЂвбжЊКЏЪ§fЃЈxЃЉЖдШЮвтxЃЌyЖМгаfЃЈx+yЃЉ=fЃЈxЃЉ+fЃЈyЃЉ-1ЃЌЧвЕБxЃО0ЪБЃЌfЃЈxЃЉЃО1ЃЌШєЙигкxЕФВЛЕШЪНfЃЈx2-ax+bЃЉЃМ1ЕФНтМЏЮЊ{x|-3ЃМxЃМ2}ЃЌдђa+b=-7 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
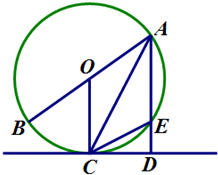 ШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌCDЪЧЁбOЕФЧаЯпЃЌCЮЊЧаЕуЃЌСЌНгACЃЌЙ§ЕуAзїADЁЭCDгкЕуDЃЌНЛЁбOгкЕуEЃЎ
ШчЭМЃЌвбжЊABЪЧЁбOЕФжБОЖЃЌCDЪЧЁбOЕФЧаЯпЃЌCЮЊЧаЕуЃЌСЌНгACЃЌЙ§ЕуAзїADЁЭCDгкЕуDЃЌНЛЁбOгкЕуEЃЎВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com