
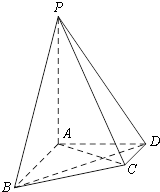
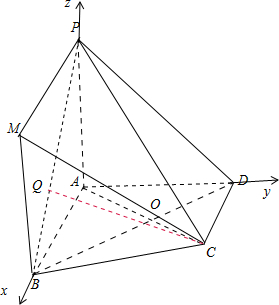
 (2013•成都模拟)在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2
(2013•成都模拟)在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AB=4,AD=2| 2 |
| ||
| 3 |
| PQ |
| PB |
42+(2
|
| 6 |
22+(2
|
| 3 |
| OD |
| OB |
| OC |
| OA |
| 2 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| 2 |
| 2 |
| PB |
| PQ |
| PB |
| QC |
| 2 |
| BD |
| 2 |
| BD |
| BD |
| QC |
| ||||
|
|
| 16λ | ||||||
2
|
| ||
| 3 |
| ||
| 3 |
| |16λ| | ||||
2
|
| 7 |
| 12 |
| PQ |
| PB |
| 7 |
| 12 |


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
| 4x |
| x2+1 |
| 1 |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•成都模拟)某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中不低于70分的学生数是
(2013•成都模拟)某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中不低于70分的学生数是查看答案和解析>>
科目:高中数学 来源: 题型:
. |
| m |
| 3 |
| x |
| 4 |
. |
| n |
| x |
| 4 |
| x |
| 4 |
. |
| m |
. |
| n |
| π |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com