
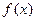 ,若存在
,若存在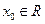 ,使
,使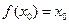 成立,则称
成立,则称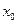 为
为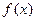 的不动点。如果
的不动点。如果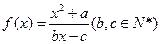 有且仅有两个不动点
有且仅有两个不动点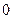 、
、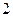 ,且
,且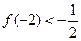 。
。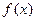 的单调区间;
的单调区间;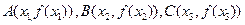 从左到右依次是函数
从左到右依次是函数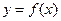 图象上三点,其中
图象上三点,其中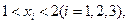 求证:⊿
求证:⊿ 是钝角三角形.
是钝角三角形.科目:高中数学 来源:不详 题型:解答题
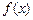 的定义域内任意的
的定义域内任意的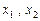 ,都有
,都有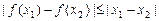 成立,那么就称函数
成立,那么就称函数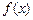 是定义域上的“平缓函数”.
是定义域上的“平缓函数”.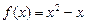 ,
,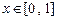 是否是“平缓函数”;(2)若函数
是否是“平缓函数”;(2)若函数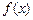 是闭区间
是闭区间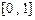 上的“平缓函数”,且
上的“平缓函数”,且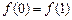 .证明:对于任意的
.证明:对于任意的
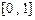 ,都有
,都有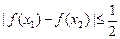 成立.(3)设
成立.(3)设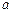 、
、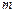 为实常数,
为实常数,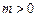 .若
.若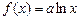 是区间
是区间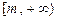 上的“平缓函数”,试估计
上的“平缓函数”,试估计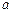 的取值范围(用
的取值范围(用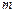 表示,不必证明).
表示,不必证明).查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
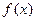 的定义域为R,若存在常数
的定义域为R,若存在常数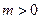 ,使
,使 对一切实数
对一切实数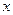 均成立,则称
均成立,则称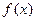 为“倍约束函数”.现给出下列函数:①
为“倍约束函数”.现给出下列函数:①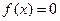 ;②
;②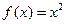 ;③
;③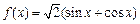 ;④
;④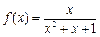 ;⑤
;⑤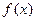 是定义在实数集R上的奇函数,且对一切
是定义在实数集R上的奇函数,且对一切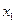 ,
,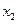 均有
均有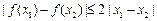 .其中是“倍约束函数”的序号是
.其中是“倍约束函数”的序号是查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(1,2) | B.(3,-1) | C.(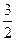 ,- ,-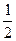 ) ) | D.(-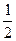 , ,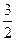 ), ), |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com