
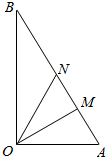
 如图所示,某镇有一块空地△OAB,其中$OA=3km,OB=3\sqrt{3}km$,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为了安全起见,需在△OAN的一周安装防护网.
如图所示,某镇有一块空地△OAB,其中$OA=3km,OB=3\sqrt{3}km$,∠AOB=90°.当地镇政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖△OMN,其中M,N都在边A,B上,且∠MON=30°,挖出的泥土堆放在△OAM地带上形成假山,剩下的△OBN地带开设儿童游乐场.为了安全起见,需在△OAN的一周安装防护网.分析 (1)由已知求出∠OAB=60°,OM=$\frac{3\sqrt{3}}{2}$,从而OM⊥AN,进而△OAN为正三角形,由此能求出防护网的总长度.
(2)设∠AOM=θ,(0°<θ<60°),由已知得ON=6$\sqrt{3}$sinθ,ON=$\frac{3\sqrt{3}}{2cosθ}$,从而6$\sqrt{3}$sin$θ=\frac{3\sqrt{3}}{2cosθ}$,由此能确定∠AOM的大小.
解答 解:(1)在△OAB中,∵OA=3,OB=3$\sqrt{3}$,∠AOB=90°,∴∠OAB=60°,
在$△AOM中,OA=3,AM=\frac{3}{2}$,∠OAM=60°,
∴由余弦定理,得OM=$\sqrt{9+\frac{9}{4}-2×3×\frac{3}{2}×cos60°}$=$\frac{3\sqrt{3}}{2}$,
∴OM2+AM2=OA2,∴OM⊥AN,∴∠AOM=30°,
∴△OAN为正三角形,∴△OAN的周长为9,
∴防护网的总长度为9km.
(2)设∠AOM=θ,(0°<θ<60°),
∵${S}_{△OMN}=\sqrt{3}{S}_{△OAM}$,
∴$\frac{1}{2}ON•OMsin30°=\sqrt{3}×\frac{1}{2}×OA×OM×sinθ$,∴ON=6$\sqrt{3}$sinθ,
在△OAN中,由$\frac{ON}{sin60°}=\frac{OA}{sin(θ+60°+30°)}$=$\frac{3}{sinθ}$,得ON=$\frac{3\sqrt{3}}{2cosθ}$,
从而6$\sqrt{3}$sin$θ=\frac{3\sqrt{3}}{2cosθ}$,∴sin2$θ=\frac{1}{2}$,
∵0°<2θ<120°,∴2θ=30°,∴θ=15°,
∴∠AOM=15°.
点评 本题考查函数在生产生活中的实际应用,是中档题,解题时要认真审题,注意正弦定理、余弦定理、勾股定理的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届湖南衡阳八中高三上学期月考二数学(理)试卷(解析版) 题型:选择题
已知函数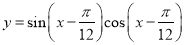 ,则下列判断正确的是( )
,则下列判断正确的是( )
A.此函数的最小正周期为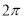 ,其图像的一个对称中心是
,其图像的一个对称中心是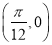
B.此函数的最小正周期为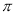 ,其图像的一个对称中心是
,其图像的一个对称中心是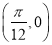
C.此函数的最小正周期为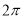 ,其图像的一个对称中心是
,其图像的一个对称中心是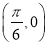
D.此函数的最小正周期为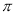 ,其图像的一个对称中心是
,其图像的一个对称中心是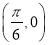
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com