
如图,三棱锥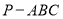 中,
中,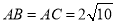 ,
,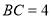 ,
,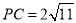 ,点
,点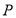 在平面
在平面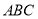 内的射影恰为
内的射影恰为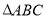 的重心
的重心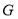 ,M为侧棱
,M为侧棱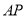 上一动点.
上一动点.
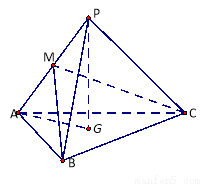
(1)求证:平面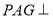 平面
平面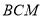 ;
;
(2)当M为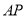 的中点时,求直线
的中点时,求直线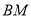 与平面
与平面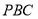 所成角的正弦值.
所成角的正弦值.
(1)详见解析;(2)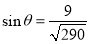 .
.
【解析】
试题分析:(1)证明平面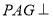 平面
平面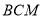 ,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面
,证明面面垂直,先证线面垂直,即证一个平面过另一个平面的垂线,本题根据面面垂直的判定定理可知在平面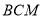 内找一条直线与平面
内找一条直线与平面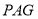 垂直,由已知
垂直,由已知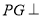 平面
平面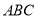 ,可得
,可得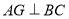 ,由题意可知,
,由题意可知,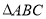 是等腰三角形,且
是等腰三角形,且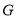 为重心,既得
为重心,既得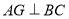 ,从而得
,从而得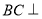 平面
平面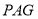 ,可证平面
,可证平面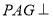 平面
平面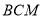 ;(2)当M为
;(2)当M为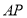 的中点时,求直线
的中点时,求直线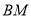 与平面
与平面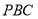 所成角的正弦值,求线面角,传统方法是找线和射影所成的角,本题找射影比较麻烦,可用向量法来求,过
所成角的正弦值,求线面角,传统方法是找线和射影所成的角,本题找射影比较麻烦,可用向量法来求,过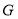 作
作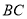 的平行线为
的平行线为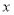 轴,
轴,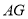 为
为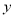 轴,
轴, 为
为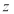 轴建立空间直角坐标系,写出各点的坐标,求出平面
轴建立空间直角坐标系,写出各点的坐标,求出平面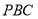 的一个法向量,利用线面角的正弦值等于线和法向量所成角的余弦值即可求出直线
的一个法向量,利用线面角的正弦值等于线和法向量所成角的余弦值即可求出直线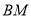 与平面
与平面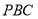 所成角的正弦值.
所成角的正弦值.
试题解析:(1)取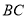 中点
中点 ,连接
,连接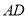 、
、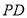 ,
,
∵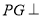 平面
平面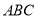 ,∴
,∴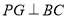
等腰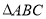 中,
中,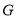 为重心,∴
为重心,∴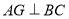
∴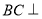 平面
平面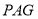
∴平面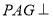 平面
平面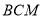 6分
6分
(2)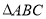 中,
中,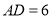 ∴
∴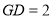
∵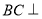 平面
平面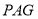 ∴
∴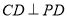
∴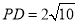 ∴
∴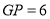
过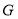 作
作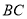 的平行线为
的平行线为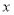 轴,
轴,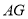 为
为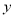 轴,
轴, 为
为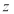 轴
轴
建立空间直角坐标系
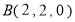
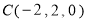
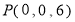
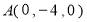
∴ 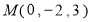
设直线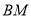 与平面
与平面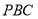 所成角为
所成角为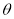
设平面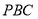 的法向量为
的法向量为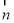

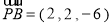 ∴
∴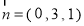

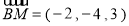 ∴
∴ 12分
12分
考点:面面垂直的判断定理,直线与平面所成的角的求法.


科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试理科数学试卷(解析版) 题型:选择题
下列四个命题:
①利用计算机产生0~1之间的均匀随机数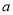 ,则事件“
,则事件“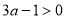 ”发生的概率为
”发生的概率为 ;
;
②“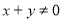 ”是“
”是“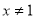 或
或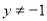 ”的充分不必要条件;
”的充分不必要条件;
③命题“在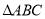 中,若
中,若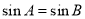 ,则
,则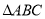 为等腰三角形”的否命题为真命题;
为等腰三角形”的否命题为真命题;
④如果平面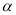 不垂直于平面
不垂直于平面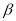 ,那么平面
,那么平面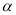 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面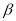 。
。
其中说法正确的个数是( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考理科数学试卷(解析版) 题型:选择题
等比数列{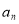 }的前n项和为
}的前n项和为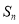 ,若
,若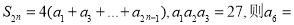 ( )
( )
A.27 B.81 C.243 D.729
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第二次联考文科数学试卷(解析版) 题型:选择题
已知等差数列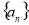 的首项为
的首项为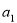 ,公差为
,公差为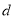 ,其前n项和为
,其前n项和为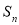 ,若直线
,若直线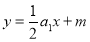 与圆
与圆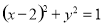 的两个交点关于直线
的两个交点关于直线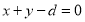 对称,则数列
对称,则数列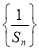 的前10项和=( )
的前10项和=( )
A.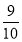 B.
B.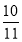 C.
C.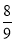 D.2
D.2
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考理科数学试卷(解析版) 题型:解答题
过双曲线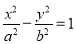
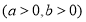 的左焦点
的左焦点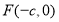
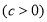 ,作倾斜角为
,作倾斜角为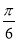 的直线
的直线 交该双曲线右支于点
交该双曲线右支于点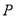 ,若
,若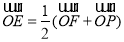 ,且
,且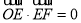 ,则双曲线的离心率为__________.
,则双曲线的离心率为__________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省盟校高三第一次联考文科数学试卷(解析版) 题型:填空题
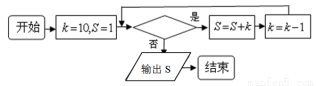
若下框图所给的程序运行结果为S=20,那么判断框中应填入的关于整数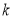 的条件是 _______________
的条件是 _______________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com