
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| C | 2 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| C | 2 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 10 |
| 27 |
| C | 2 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 8 |
| 27 |
| X | 3 | 4 | 5 | ||||||
| P |
|
|
|
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
| 107 |
| 27 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
| A、4 | B、3 | C、2 | D、1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、[-1,1] |
| B、(-3,-1) |
| C、{-1,0,1} |
| D、{0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| A、135° | B、45° |
| C、135°或45° | D、90° |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
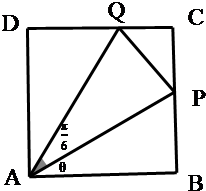 如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=
如图,某污水处理厂要在一正方形污水处理池ABCD内修建一个三角形隔离区以投放净化物质,其形状为三角形APQ,其中P位于边CB上,Q位于边CD上.已知AB=20米,∠PAQ=| π |
| 6 |
| 正方形ABCD面积 |
| APAQ面积 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com