
已知a∈R,函数f(x)=4x3-2ax+a.
(1)求f(x)的单调区间;
(2)证明:当0≤x≤1时,f(x)+|2-a|>0.
(1) 函数f(x)的单调递增区间为 和
和 ,
,
单调递减区间为 .
.
(2)见解析
【解析】(1)由题意得f′(x)=12x2-2a.
当a≤0时,f′(x)≥0恒成立,此时f(x)的单调递增区间为(-∞,+∞).
当a>0时,f′(x)=12
 ,
,
此时函数f(x)的单调递增区间为 和
和 ,
,
单调递减区间为 .
.
(2)证明:由于0≤x≤1,故当a≤2时,f(x)+|a-2|=4x3-2ax+2≥4x3-4x+2.
当a>2时,f(x)+|a-2|=4x3+2a(1-x)-2≥4x3+4(1-x)-2=4x3-4x+2.
设g(x)=2x3-2x+1,0≤x≤1,则
g′(x)=6x2-2=6
 .
.
于是
x | 0 |
|
|
| 1 |
g′(x) |
| - | 0 | + |
|
g(x) | 1 | 减 | 极小值 | 增 | 1 |
所以g(x)min=g =1-
=1- >0.
>0.
所以当0≤x≤1时,2x3-2x+1>0.
故f(x)+|a-2|≥4x3-4x+2>0.


科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题3第2课时练习卷(解析版) 题型:解答题
已知等比数列{an}的所有项均为正数,首项a1=1,且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:选择题
在四边形ABCD中,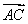 =(1,2),
=(1,2),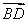 =(-4,2),则该四边形的面积为( )
=(-4,2),则该四边形的面积为( )
A.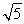 B.2
B.2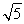 C.5 D.10
C.5 D.10
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:解答题
已知函数f(x)=4cos x·sin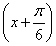 +a的最大值为2.
+a的最大值为2.
(1)求a的值及f(x)的最小正周期;
(2)求f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第1课时练习卷(解析版) 题型:选择题
三角形ABC是锐角三角形,若角θ终边上一点P的坐标为(sin A-cos B,cos A-sin C),则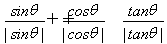 的值是( )
的值是( )
A.1 B.-1 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:解答题
设f(x)=aln x+ +
+ x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
x+1,其中a∈R,曲线y=f(x)在点(1,f(1))处的切线垂直于y轴.
(1)求a的值;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第5课时练习卷(解析版) 题型:选择题
函数f(x)的定义域为(0,+∞),且f(x)>0,f′(x)>0,则函数y=xf(x)( )
A.存在极大值 B.存在极小值
C.是增函数 D.是减函数
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第3课时练习卷(解析版) 题型:解答题
设函数f(x)=ax2+bx+b-1(a≠0).
(1)当a=1,b=-2时,求函数f(x)的零点;
(2)若对任意b∈R,函数f(x)恒有两个不同零点,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题四练习卷(解析版) 题型:解答题
已知等比数列{an}的所有项均为正数,首项a1=1,且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com