
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的定区间,从而求出函数的极值即可;
(2)根据(1)取a=1,得到lnx≤x-1,令x=n,得到$\frac{lnn}{n+1}<\frac{n-1}{n+1}$,从而证出结论.
解答 解:(1)f(x)的定义域为(0,+∞),
$f'(x)=\frac{1-(lnx+a)}{x^2}$,令f'(x)=0,解得:x=e1-a,
当f'(x)>0时,x<e1-a,f(x)在(0,e1-a)是增函数,
当f'(x)<0时,x>e1-a,f(x)在(e1-a,+∞)是减函数,
∴f(x)在x=e1-a处取得极大值,f(x)极大值=f(e1-a)=ea-1,无极小值.
(2)证明:由(1)$f(x)=\frac{lnx+a}{x}$≤ea-1,
取a=1,∴lnx≤x-1,当x=1时取等号,
令x=n,∵n≥2,故$\frac{lnn}{n+1}<\frac{n-1}{n+1}$
∴$\frac{ln2•ln3…lnn}{(n+1)!}=\frac{1}{2}•\frac{ln2}{3}•\frac{ln3}{4}…\frac{lnn}{n+1}<\frac{1}{2}•\frac{1}{3}•\frac{2}{4}•\frac{3}{5}•\frac{4}{6}…\frac{n-2}{n}•\frac{n-1}{n+1}$=$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$
故$\frac{ln2}{6}<\frac{1}{2}-\frac{1}{3}$;$\frac{ln2•ln3}{24}<\frac{1}{3}-\frac{1}{4}$;…;
$\frac{ln2•ln3…lnn}{(n+1)!}$<$\frac{1}{n}-\frac{1}{n+1}$
∴$\frac{ln2}{6}+\frac{ln2•ln3}{24}+…+\frac{ln2•ln3…lnn}{(n+1)!}<\frac{n-1}{2n+2},n≥2$.
点评 本题考查了函数的单调性问题,考查导数的应用,不等式的证明,转化思想,是一道综合题.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:选择题
| A. | z在复平面内对应的点在第一象限 | B. | |z|=$\sqrt{2}$ | ||
| C. | z的虚部是i | D. | z的实部是1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
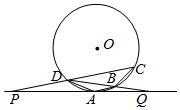 如图,四边形ABCD是⊙O的内接四边形,且AB∥CD,过点A作⊙O的切线,与CD,DB的延长线分别交于点P,Q.
如图,四边形ABCD是⊙O的内接四边形,且AB∥CD,过点A作⊙O的切线,与CD,DB的延长线分别交于点P,Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
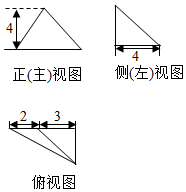 已知某几何体的三视图如图所示,则该几何体的体积是( )
已知某几何体的三视图如图所示,则该几何体的体积是( )| A. | 28+6$\sqrt{5}$ | B. | 40 | C. | $\frac{40}{3}$ | D. | 30+6$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com