
分析 (1)由圆C:x2+y2-4x+3=0配方可得:(x-2)2+y2=1,可得圆心C(2,0).可得抛物线的焦点F(2,0).因此$\frac{p}{2}$=2,解得p,即可得出.
(2)设直线l的方程为:my+t=x,A(x1,y1),B(x2,y2).由直线l与圆C相切,可得:(t-2)2=m2+1≥1.t≥3,或t≤1.
联立$\left\{\begin{array}{l}{my+t=x}\\{{y}^{2}=8x}\end{array}\right.$,化为:y2-8my-8t=0,△>0.进而得到t≥3,或-2m2<t≤1.利用数量积运算性质、根与系数的关系可得:$\overrightarrow{FA}•\overrightarrow{FB}$=(x1-2)(x2-2)+y1y2═-15t2+52t-44=$-15(t-\frac{26}{15})^{2}$+$\frac{16}{15}$,再利用二次函数的单调性即可得出.
解答 解:(1)由圆C:x2+y2-4x+3=0配方可得:(x-2)2+y2=1,可得圆心C(2,0).
∴抛物线的焦点F(2,0).
∴$\frac{p}{2}$=2,解得p=4.
∴抛物线的准线方程为:x=-2.
(2)设直线l的方程为:my+t=x,A(x1,y1),B(x2,y2).
∵直线l与圆C相切,∴$\frac{|2-t|}{\sqrt{{m}^{2}+1}}$=1,化为:(t-2)2=m2+1≥1.
∴t≥3,或t≤1.
联立$\left\{\begin{array}{l}{my+t=x}\\{{y}^{2}=8x}\end{array}\right.$,化为:y2-8my-8t=0,
△=64m2+32t>0.∴t>-2m2.
∴t≥3,或-2m2<t≤1.
∴y1+y2=8m,y1y2=-8t.
∴$\overrightarrow{FA}•\overrightarrow{FB}$=(x1-2)(x2-2)+y1y2=(my1+t-2)(my2+t-2)+y1y2
=(m2+1)y1y2+m(t-2)(y1+y2)+(t-2)2
=-8t(m2+1)+8m2(t-2)+(t-2)2
=-8t(t-2)2+8[(t-2)2-1](t-2)+(t-2)2
=-15t2+52t-44
=$-15(t-\frac{26}{15})^{2}$+$\frac{16}{15}$∈(-∞,-7].
∴$\overrightarrow{FA}•\overrightarrow{FB}$的取值范围是(-∞,-7].
点评 本题考查了抛物线与圆的标准方程及其性质、直线与圆相切的性质、直线与抛物线相交问题、向量数量积运算性质、二次函数的单调性,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 2 | 3 | 4 | 5 | 6 | 7 | … |
| 3 | 5 | 7 | 9 | 11 | 13 | … |
| 4 | 7 | 10 | 13 | 16 | 19 | … |
| 5 | 9 | 13 | 17 | 21 | 25 | … |
| 6 | 11 | 16 | 21 | 26 | 31 | … |
| 7 | 13 | 19 | 25 | 31 | 37 | … |
| … | … | … | … | … | … | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
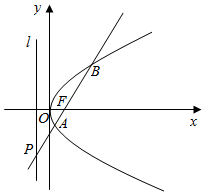 已知抛物线C:y2=2px(p>0),其焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线于P点.
已知抛物线C:y2=2px(p>0),其焦点为F(1,0),过F作斜率为k的直线交抛物线C于A、B两点,交其准线于P点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com