证明::(1)令h(x)=f(x)-x,则h′(x)=f′(x)-1<0,故h(x)是单调递减函数,
所以,方程h(x)=0,即f(x)-x=0至多有一解,
又由题设①知方程f(x)-x=0有实数根,
所以,方程f(x)-x=0有且只有一个实数根
(2)易知,g′(x)=

-

,则0<g′(x)<1,满足条件②;
令F(x)=g(x)-x=
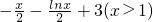
,
则F(e)=
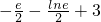
=
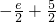
>0,F(e
2)=
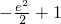
<0,
又F(x)在区间[e,e
2]上连续,所以F(x)在[e,e
2]上存在零点x
0,
即方程g(x)-x有实数根x
0∈[e,e
2],故g(x)满足条件①,
综上可知,g(x)∈M
(Ⅲ)不妨设α≤β,∵f′(x)>0,∴f(x)单调递增,
∴f(α)≤f(β),即f(β)-f(α)≥0,
令h(x)=f(x)-x,则h′(x)=f′(x)-1<0,故h(x)是单调递减函数,
∴f(β)-β≤f(α)-α,即f(β)-f(α)≤β-α,
∴0≤f(β)-f(α)≤β-α,
则有|f(α)-f(β)|≤|α-β|.
分析:(1)构造函数h(x)=f(x)-x,由已知可判断h(x)是单调递减函数,由单调函数至多有一个零点,及方程f(x)-x=0有实根,可证得答案;
(2)结合函数g(x)=
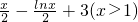
,分析条件:①方程g(x)-x=0有实根;②函数g(x)的导数g′(x)满足0<g′(x)<1.两个条件是否满足,可得结论;
(3)不妨设α≤β,由(1)证得函数的单调性,易证明0≤f(β)-f(α)≤β-α,进而根据绝对值的定义得到结论.
点评:本题是函数与方程的综合应用,是函数零点与方程根关系的综合应用,其中利用导数法分析函数的单调性,进而判断函数零点的个数及对应方程根的个数难度较大.

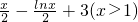 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; -
- ,则0<g′(x)<1,满足条件②;
,则0<g′(x)<1,满足条件②;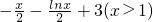 ,
,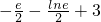 =
=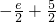 >0,F(e2)=
>0,F(e2)=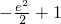 <0,
<0,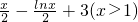 ,分析条件:①方程g(x)-x=0有实根;②函数g(x)的导数g′(x)满足0<g′(x)<1.两个条件是否满足,可得结论;
,分析条件:①方程g(x)-x=0有实根;②函数g(x)的导数g′(x)满足0<g′(x)<1.两个条件是否满足,可得结论;

 阅读快车系列答案
阅读快车系列答案