
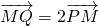 .
.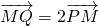 ,
, ,
,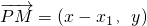
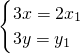 ?
?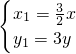
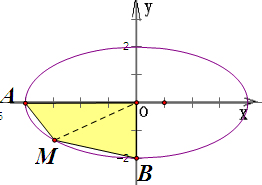
 ,
,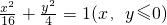 即为点M的轨迹方程;
即为点M的轨迹方程;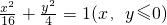 上,
上, OA×|yM|=-4sinα,S△OBM=
OA×|yM|=-4sinα,S△OBM= OB×|xM|=-4cosα
OB×|xM|=-4cosα ≤(sinα+cosα)≤
≤(sinα+cosα)≤
 时,sinα+cosα的最小值为-
时,sinα+cosα的最小值为-

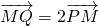 ,解出用x、y表示x1,y1的式子,最后根据线段PQ长为6建立关系式,再结合点P、Q分别在射线y=0(x≤0)和x=0(y≤0)上滑动,可得点M的轨迹方程;
,解出用x、y表示x1,y1的式子,最后根据线段PQ长为6建立关系式,再结合点P、Q分别在射线y=0(x≤0)和x=0(y≤0)上滑动,可得点M的轨迹方程; ,从而得到四边形OAMB面积的最大值.
,从而得到四边形OAMB面积的最大值.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4
如图,某市拟在长为16km的道路OP的一侧修建一条自行车赛道,赛道的前一部分为曲线OSM,该曲线段为函数y=Asinωx(A>0,ω>0,x∈[0,8]的图象,且图象的最高点为S(6,4| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
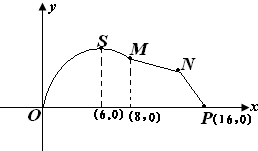
 如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )
如图,在棱长为4的正方体ABCD-A′B′C′D′中,E、F分别是AD、A′D′的中点,长为2的线段MN的一个端点M在线段EF上运动,另一个端点N在底面A′B′C′D′上运动,则线段MN的中点P的轨迹(曲面)与二面角A-A′D′-B′所围成的几何体的体积为( )查看答案和解析>>
科目:高中数学 来源: 题型:
 已知椭圆E:
已知椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
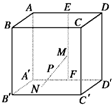
 如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=
如图所示,在四棱锥P-ABCD中,底面四边形ABCD是菱形,AC∩BD=O,△PAC是边长为2的等边三角形,PB=PD=| 6 |
| BM |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
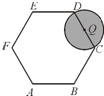 如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量
如图,在边长为2的正六边形ABCDEF中,动圆Q的半径为1,圆心在线段CD(含端点)上运动,P是圆Q上及内部的动点,设向量| AP |
| AB |
| AF |
| A、(1,2] |
| B、[5,6] |
| C、[2,5] |
| D、[3,5] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com