
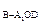 =
=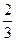
 , ∵OO
, ∵OO ⊥平面AOB,∴OO
⊥平面AOB,∴OO ⊥AO
⊥AO ,又AO⊥OB
,又AO⊥OB  B
B B
B 为A B
为A B 在平面OO
在平面OO B
B B内的射影
B内的射影 ∴四边形OO
∴四边形OO B
B B为正方形
B为正方形 ⊥OB
⊥OB
 ⊥A B
⊥A B (三垂线定理)分
(三垂线定理)分 交OA
交OA 于E,再连结DE.
于E,再连结DE. O
O O为矩形 ,∴E为A O
O为矩形 ,∴E为A O 的中点.
的中点. ∥D……………6分
∥D……………6分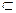 平面OA
平面OA D,BO
D,BO
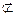 平面OA
平面OA D
D ∥平面OA
∥平面OA D
D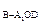 = V
= V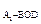 ,
,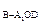 =
=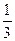 ·S
·S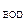 ·A
·A A。
A。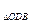 =
=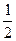 ·S
·S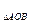 =1,A1A=2,
=1,A1A=2,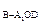 =
=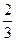 。
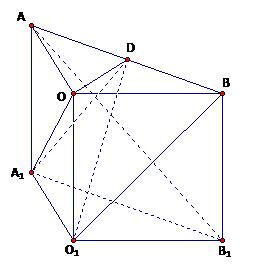
。 为原点建立如图所示的空间直角坐标系,则:
为原点建立如图所示的空间直角坐标系,则: (0,0,0),A
(0,0,0),A (2,0,0),B
(2,0,0),B (0,2,0),A(2,0,2),
(0,2,0),A(2,0,2),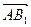 =(-2,2,-2),
=(-2,2,-2),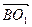 =(0,-2,-2)
=(0,-2,-2)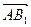 ·
·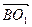 ="(-2)" ·0+2·(-2)+(-2) ·(-2)=0
="(-2)" ·0+2·(-2)+(-2) ·(-2)=0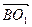 ⊥
⊥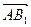 ∴B O
∴B O ⊥A B
⊥A B
 的中点为E,则E点的坐标是(1,0,1),∴
的中点为E,则E点的坐标是(1,0,1),∴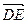 ="(0,-1,-1), " 又
="(0,-1,-1), " 又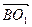 =(0,-2,-2)
=(0,-2,-2)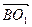 =2
=2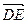 又BO
又BO 、DE不共线, ∴BO
、DE不共线, ∴BO ∥DE
∥DE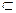 平面OA
平面OA D,BO
D,BO
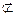 平面OA
平面OA D ∴BO
D ∴BO ∥平面OA
∥平面OA D③与证法1相同
D③与证法1相同

科目:高中数学 来源:不详 题型:解答题
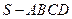 的底面是边长为
的底面是边长为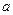 的正方形,且
的正方形,且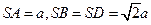 。
。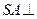 平面
平面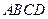 ;
;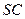 为四棱锥中最长的侧棱,点
为四棱锥中最长的侧棱,点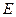 为
为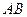 的中点.求直线SE.与平面SAC所成角的正弦值。
的中点.求直线SE.与平面SAC所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
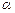 ,直线
,直线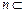 平面
平面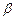 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )| A.若α∥β,则m⊥n | B.若α⊥β,则m∥n |
| C.若m⊥n,则α∥β | D.若n∥α,则α∥β |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.点P必在直线AC上 | B.点P必在直线BD上 |
| C.点P必在平面DBC外 | D.点P必在平面ABC内 |
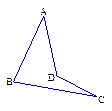
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com