
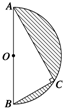
 如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积. 分析 求出AC=$\sqrt{3}$R,BC=R,CO1=$\frac{\sqrt{3}}{2}$R,再求出几何体的表面积;要求旋转后阴影部分的体积即是球的体积减去两个圆锥的体积,根据圆锥的体积公式和球的体积公式进行计算.
解答 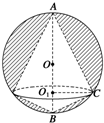 解:如图所示,过C作CO1⊥AB于O1,在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R,
解:如图所示,过C作CO1⊥AB于O1,在半圆中可得∠BCA=90°,∠BAC=30°,AB=2R,
∴AC=$\sqrt{3}$R,BC=R,CO1=$\frac{\sqrt{3}}{2}$R,
∴S球=4πR2,
${S}_{圆锥A{O}_{1}侧}$=π×$\frac{\sqrt{3}}{2}$R×$\sqrt{3}$R=$\frac{3}{2}$πR2,
${S}_{圆锥B{O}_{1}侧}$=π×$\frac{\sqrt{3}}{2}$R×R=$\frac{\sqrt{3}}{2}$πR2,
∴S几何体表=S球+${S}_{圆锥A{O}_{1}侧}$+${S}_{圆锥B{O}_{1}侧}$=$\frac{11+\sqrt{3}}{2}$πR2,
∴旋转所得到的几何体的表面积为$\frac{11+\sqrt{3}}{2}$πR2.
又V球=$\frac{4}{3}$πR3,${V}_{圆锥A{O}_{1}}$=$\frac{1}{3}$•AO1•π•CO12=$\frac{1}{4}$πR2•AO1
${V}_{圆锥B{O}_{1}}$=$\frac{1}{3}$BO1•πCO12=$\frac{1}{4}$BO1•πR2
∴V几何体=V球-(${V}_{圆锥A{O}_{1}}$+${V}_{圆锥B{O}_{1}}$)=$\frac{5}{6}$πR3.
点评 本题考查组合体的表面积、体积的求法,能够熟练运用锐角三角函数的概念进行求解,熟悉圆锥和球的表面积、体积公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-14,16) | B. | (22,-11) | C. | (6,1) | D. | (2,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{12}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{30}$ | D. | $\frac{2}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
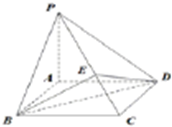 在四棱锥P-ABCD中,设底面ABCD是边长为1的正方形,PA⊥面ABCD.
在四棱锥P-ABCD中,设底面ABCD是边长为1的正方形,PA⊥面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 12 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com