
在△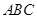 中,内角
中,内角 所对的边分别为
所对的边分别为 ,已知m
,已知m ,n
,n ,m·n
,m·n .
.
(1)求 的大小;
的大小;
(2)若 ,
, ,求△
,求△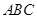 的面积.
的面积.
(1)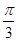 ;(2)
;(2)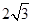 .
.
解析试题分析:(1)由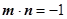 ,结合向量数量积的定义,可得关于
,结合向量数量积的定义,可得关于 的三角函数关系式,然后对三角函数关系式进行适当变形处理,直到能求出
的三角函数关系式,然后对三角函数关系式进行适当变形处理,直到能求出 的某个三角函数即可;(2)本题本质上就是一个解三角形的问题,沟通三角形中的边角关系主要是正弦定理和余弦定理,在
的某个三角函数即可;(2)本题本质上就是一个解三角形的问题,沟通三角形中的边角关系主要是正弦定理和余弦定理,在 中,已知
中,已知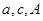 ,求其面积,可先用余弦定理求出
,求其面积,可先用余弦定理求出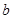 ,再用面积公式求出面积,也可先用正弦定理求出
,再用面积公式求出面积,也可先用正弦定理求出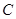 ,再得
,再得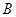 ,进而用三角形面积公式求出面积.
,进而用三角形面积公式求出面积.
试题解析:解:(1)法一:由题意知m·n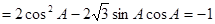 .
.
∴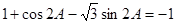 . 即
. 即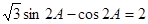 ,∴
,∴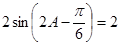 ,即
,即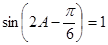 .
.
∵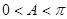 ,∴
,∴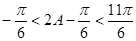 ,∴
,∴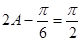 ,即
,即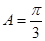 .
.
法二:由题意知m·n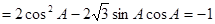 .
.
∴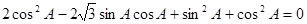 即
即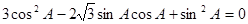 .
.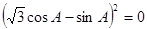 ∴
∴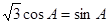 ,即
,即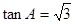 ,∵
,∵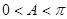 ,∴
,∴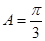 .
.
(2)法一:由余弦定理知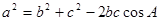 ,即
,即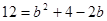 ,
,
∴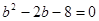 ,解得
,解得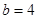 ,(
,(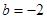 舍去)
舍去)
∴△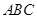 的面积为
的面积为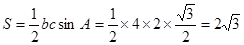 .
.
法二:由正弦定理可知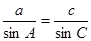 ,所以
,所以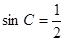 ,因为
,因为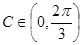
所以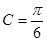 ,
,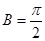 .∴△
.∴△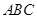 的面积为
的面积为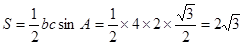


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)如图,在△ABC中,∠ABC=90°,AB= ,BC=1,P为△ABC内一点,∠BPC=90°
,BC=1,P为△ABC内一点,∠BPC=90°
(1)若PB= ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,有两座建筑物AB和CD都在河的对岸(不知 道它们的高度,且不能到达对岸),某人想测量两 座建筑物尖顶A、C之间的距离,但只有卷尺和测 角仪两种工具.若此人在地面上选一条基线EF,用 卷尺测得EF的长度为a,并用测角仪测量了一些角度: ,
, ,
, ,
, ,
, 请你用文字和公式写出计算A、C之间距离的步骤和结果.
请你用文字和公式写出计算A、C之间距离的步骤和结果.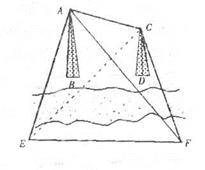
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com