练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中，设
    AB
    =（2，3），
    AC
    =（3，k），且△ABC为直角三角形，求实数k的值．
    考点：数量积判断两个平面向量的垂直关系
    专题：平面向量及应用
    分析：分A、B、C分别为直角，由相应的向量的数量积为0，解方程可得k值．
    解答： 解：若A=90°，由
    AB
    •
    AC
    =0    ，得2×3+3k=0，解得k=-2；
    若B=90°，
    BC
    =
    AC
    -
    AB
    =(1 ， k-3)    ，由
    AB
    •
    BC
    =0    ，
    得2×1+3（k-3）=0，解得k=
    7
    3
    ；
    若C=90°，由
    AC
    •
    BC
    =0    ，得1×3+k（k-3）=0，即k2-3k+3=0，方程无实根，
    综上可得k的值为：-2或
    7
    3
    点评：本题考查数量积与向量垂直的关系，涉及分类讨论的思想，属易错题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列各式中正确的是（　　）
    （1）（λ•
    a
    ）•
    b
    =λ•（
    a
    b
    ）=
    a
    •（λ
    b
    ）
    （2）|
    a
    •
    b
    |=|
    a
    |•|
    b
    |
    （3）（
    a
    •
    b
    ）•
    c
    =
    a
    •（
    b
    •
    c
    ）
    （4）（
    a
    +
    b
    ）•
    c
    =
    a
    •
    c
    +
    b
    •
    c
    ．
    A、（1）（3）
    B、（2）（4）
    C、（1）（4）
    D、以上都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：

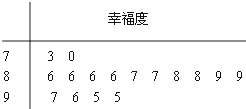    前不久，省社科院发布了2013年度“安徽城市居民幸福排行榜”，芜湖市成为本年度安徽最“幸福城”．随后，师大附中学生会组织部分同学，用“10分制”随机调查“阳光”社区人们的幸福度．现从调查人群中随机抽取16名，如图所示的茎叶图记录了他们的幸福度分数（以小数点前的一位数字为茎，小数点后的一位数字为叶）：
    （Ⅰ）指出这组数据的众数和中位数；
    （Ⅱ）若幸福度不低于9.5分，则称该人的幸福度为“极幸福”．求从这16人中随机选取3人，至多有1人是“极幸福”的概率；
    （Ⅲ）以这16人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选3人，记ξ表示抽到“极幸福”的人数，求ξ的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）求f(x)=
    		x2-4x+3
    +
    3
    		-x2-7x+8
    的定义域．
    （2）画出y=|x-1|+|x+2|的图象，并写出它的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    		3
    sin2x+2cos2x．
    （1）将f（x）的图象向右平移
    π
    12
    个单位长度，再将周期扩大一倍，得到函数g（x）的图象，求g（x）的解析式；
    （2）求函数f（x）的最小正周期和单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

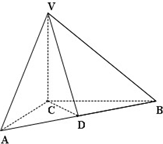    如图，在三棱锥V-ABC中，VC⊥底面ABC，AC⊥BC，D为AB的中点，且AC=BC=VC=a．
    （Ⅰ）求证：AB⊥平面VCD；
    （Ⅱ）求点C到平面VAB的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设a为正实数，函数f（x）=2x2+（x-a）|x-a|．
    （Ⅰ）若f（0）≤-1，求a的取值范围；
    （Ⅱ）求f（x）的最小值；
    （Ⅲ）若x∈（a，+∞），求不等式f（x）≥1的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知△ABC的面积为
    1
    2
    ，且b=2，c=1，则A=
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在Rt△ABC中，∠ACB=90°，AC=6，BC=3，D、E分别在边AB、AC上，且
    DB
    =2
    AD
    ，
    AC
    =3
    EC
    ，则
    CD
    •
    BE
    =
     
    ．

    查看答案和解析>>

    同步练习册答案