
分析 (I)利用椭圆的定义及其标准方程即可得出.
(Ⅱ)设A1(x1,y1),B(x2,y2),直线方程与椭圆方程联立化为:7x2-8x-8=0,利用弦长公式|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$即可得出.
解答 解:(Ⅰ)∵点P到两定点F1,F2的距离之和为4大于两定点间的距离|F1F2|=2,
∴点P的轨迹是以F1,F2为焦点的椭圆,其设其方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$,
则2a=4,2c=2
即$a=2,c=1,b=\sqrt{3}$
∴点P的轨迹方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
(Ⅱ)设A1(x1,y1),B(x2,y2),联立$\left\{\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{3}=1\\ y=x-1\end{array}\right.$,得7x2-8x-8=0,
则有$\left\{\begin{array}{l}{x_1}+{x_2}=\frac{8}{7}\\{x_1}{x_2}=-\frac{8}{7}\end{array}\right.$,
∴弦长|AB|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{2[(\frac{8}{7})^{2}+4×\frac{8}{7}]}$=$\frac{24}{7}$.
点评 本题考查了椭圆的定义标准方程及其性质、直线与椭圆相交弦长问题、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 第十届珠海航展与10月28日至11月1日在珠海市机场路航展馆举行,组委会为了做好接待工作,对参加服务的200名工作人员进行为期一周的培训,培训结束对服务人员进行珠海航展知识测评,其成绩的频率分布直方图如图所示,规定95分及其以上获优胜奖.
第十届珠海航展与10月28日至11月1日在珠海市机场路航展馆举行,组委会为了做好接待工作,对参加服务的200名工作人员进行为期一周的培训,培训结束对服务人员进行珠海航展知识测评,其成绩的频率分布直方图如图所示,规定95分及其以上获优胜奖.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 10 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
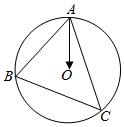
 如图,给出了一个算法框图,其作用是输入x的值,输出相应的y的值,若要使输入的x值与输出的y值相等,则这样的x的值有( )
如图,给出了一个算法框图,其作用是输入x的值,输出相应的y的值,若要使输入的x值与输出的y值相等,则这样的x的值有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
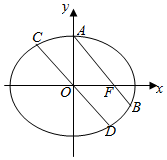 如图,点A,F分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点和右焦点,过中心O作直线AF的平行线交椭圆于C,D两点,若CD的长是焦距的$\frac{{4\sqrt{5}}}{5}$倍,则该椭圆的离心率为$\frac{1}{2}$.
如图,点A,F分别是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点和右焦点,过中心O作直线AF的平行线交椭圆于C,D两点,若CD的长是焦距的$\frac{{4\sqrt{5}}}{5}$倍,则该椭圆的离心率为$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com