样本中共有5个个体.其值分别为.若该样本的平均值为1.则样本方差为A．B．C．D．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

样本中共有5个个体，其值分别为

.若该样本的平均值为1，则样本方差为

A．

B．

C．

D．

试题分析：根据题意，由于样本中共有5个个体，其值分别为

.若该样本的平均值为1，则可知a+0+1+2+3=5,a=-1,那么方差为

，故答案为D.
点评：主要是考查了数据的特征数，均值和方差的求解，属于基础题。

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：不详 题型：解答题

中国航母“辽宁舰”是中国第一艘航母，“辽宁”号以4台蒸汽轮机为动力,为保证航母的动力安全性，科学家对蒸汽轮机进行了170余项技术改进，增加了某项新技术，该项新技术要进入试用阶段前必须对其中的三项不同指标甲、乙、丙进行通过量化检测。假如该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为

、

。指标甲、乙、丙合格分别记为4分、2分、4分；若某项指标不合格，则该项指标记0分，各项指标检测结果互不影响。
(I)求该项技术量化得分不低于8分的概率；
(II)记该项新技术的三个指标中被检测合格的指标个数为随机变量X,求X的分布列与数学期望。

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

某社团组织

名志愿者利用周末和节假日参加社会公益活动,活动内容是：1、到各社区宣传慰问,倡导文明新风；2、到指定的医院、福利院做义工,帮助那些需要帮助的人.各位志愿者根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示：

	宣传慰问	义工	总计
20至40岁	11	16	27
大于40岁	15	8	23
总计	26	24	50

(1) 分层抽样方法在做义工的志愿者中随机抽取6名,年龄大于40岁的应该抽取几名?
(2) 上述抽取的6名志愿者中任取2名,求选到的志愿者年龄大于40岁的人数的数学期望.

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

甲、乙两人各进行3次射击，甲每次击中目标的概率为

，乙每次击中目标的概率为

.
(1)求乙至多击中目标2次的概率；
(2)记甲击中目标的次数为Z，求Z的分布列、数学期望和标准差．

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判，设各局中双方获胜的概率均为

各局比赛的结果都相互独立，第

局甲当裁判.
（I）求第

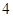局甲当裁判的概率；
（II）求前

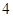局中乙恰好当

次裁判概率.

查看答案和解析>>

科目：高中数学 来源：不详 题型：解答题

某食品加工厂甲，乙两个车间包装小食品，在自动包装传送带上每隔30分钟抽取一袋食品，称其重量并将数据记录如下：
甲：102 100 98 97 103 101 99
乙： 102 101 99 98 103 98 99
（1）食品厂采用的是什么抽样方法（不必说明理由）？
（2）根据数据估计这两个车间所包装产品每袋的平均质量；
（3）分析哪个车间的技术水平更好些？
附：