
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
| 天数x/天 | 1 | 2 | 3 | 4 | 5 | 6 |
| 繁殖个数y/个 | 6 | 12 | 25 | 49 | 95 | 190 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2015-2016学年辽宁大连十一中高一下学期段考二试数学(文)试卷(解析版) 题型:解答题
已知向量 =(2cosωx,-1),
=(2cosωx,-1),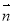 =(sinωx-cosωx,2)( ω>0),函数f(x)=
=(sinωx-cosωx,2)( ω>0),函数f(x)=  ·
·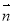 +3,若函数f(x)的图象的两个相邻对称中心的距离为
+3,若函数f(x)的图象的两个相邻对称中心的距离为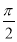 .
.
(Ⅰ)求函数f(x)的单调增区间;
(Ⅱ)若将函数f(x)的图象先向左平移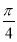 个单位,然后纵坐标不变,横坐标缩短为原来的
个单位,然后纵坐标不变,横坐标缩短为原来的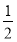 倍,得到函数g(x)的图象,当x∈[
倍,得到函数g(x)的图象,当x∈[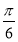 ,
,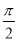 ]时,求函数g(x)的值域.
]时,求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源:2017届重庆市高三文上适应性考试一数学试卷(解析版) 题型:解答题
选修4-1:几何证明选讲
如图,在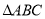 中,
中,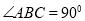 ,以
,以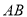 为直径的圆交
为直径的圆交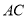 于点
于点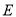 ,过点
,过点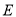 作圆
作圆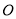 的切线交
的切线交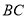 于点
于点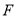 .
.

(1)求证: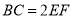 ;
;
(2)若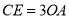 ,求
,求 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com