
【题目】在湖南师大附中的校园歌手大赛决赛中,有6位参赛选手(1号至6号)登台演出,由现场的100位同学投票选出最受欢迎的歌手,各位同学须彼此独立地在投票器上选出3位侯选人,其中甲同学是1号选手的同班同学,必选1号,另在2号至6号选手中随机选2名;乙同学不欣赏2号选手,必不选2号,在其他5位选手中随机选出3名;丙同学对6位选手的演唱没有偏爱,因此在1号至6号选手中随机选出3名.
(1)求同学甲选中3号且同学乙未选中3号选手的概率;
(2)设3号选手得到甲、乙、丙三位同学的票数之和为X,求X的分布列和数学期望.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)设A表示事件:“甲选中3号歌手”,事件B表示“乙选中3号歌手”,事件C表示“丙选中3号歌手”,由等可能事件概率公式求出P(A),P(B),由此利用相互独立事件的概率乘法公式和对立事件的概率公式能求出概率.
(2)先由等可能事件概率计算公式求出P(C),由已知得X的可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列及数学期望.
设![]() 表示事件“甲同学选中3号选手”,
表示事件“甲同学选中3号选手”,![]() 表示事件“乙同学选中3号选手”,
表示事件“乙同学选中3号选手”,![]() 表示事件“丙同学选中3号选手”,则
表示事件“丙同学选中3号选手”,则
(1)![]() ,
,![]() ,
,
所以![]() .
.
(2)![]() ,
,
![]() 可能的取值为0,1,2,3,
可能的取值为0,1,2,3,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() .
.
所以![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
![]() 的数学期望
的数学期望![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A. 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人
B. 由三角形的性质,推测空间四面体的性质
C. 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D. 在数列![]() 中,
中,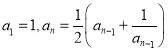 ,可得
,可得![]() ,由此归纳出
,由此归纳出![]() 的通项公式
的通项公式![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 为
为![]() 的焦点.
的焦点.
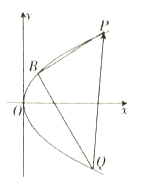
(1)若![]() ,
,![]() 是
是![]() 上的两点,证明:
上的两点,证明:![]() ,
,![]() ,
,![]() 依次成等比数列.
依次成等比数列.
(2)过![]() 作两条互相垂直的直线与
作两条互相垂直的直线与![]() 的另一个交点分别交于
的另一个交点分别交于![]() ,
,![]() (
(![]() 在
在![]() 的上方),求向量
的上方),求向量![]() 在
在![]() 轴正方向上的投影的取值范围.
轴正方向上的投影的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位幼儿园老师给班上k(k≥3)个小朋友分糖果.她发现糖果盒中原有糖果数为a0,就先从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的
分给第一个小朋友;再从别处抓2块糖加入盒中,然后把盒内糖果的![]() 分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的
分给第二个小朋友;…,以后她总是在分给一个小朋友后,就从别处抓2块糖放入盒中,然后把盒内糖果的![]() 分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
分给第n(n=1,2,3,…k)个小朋友.如果设分给第n个小朋友后(未加入2块糖果前)盒内剩下的糖果数为an.
(1)当k=3,a0=12时,分别求a1,a2,a3;
(2)请用an-1表示an;令bn=(n+1)an,求数列{bn}的通项公式;
(3)是否存在正整数k(k≥3)和非负整数a0,使得数列{an}(n≤k)成等差数列,如果存在,请求出所有的k和a0,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设动直线![]() :
:![]() 分别与曲线
分别与曲线![]() ,
,![]() 相交于点
相交于点![]() ,
,![]() ,求当
,求当![]() 为何值时,
为何值时,![]() 取最大值,并求
取最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学在全校范围内举办了一场“中国诗词大会”的比赛,规定初赛测试成绩不小于160分的学生进入决赛阶段比赛.现有200名学生参加测试,并将所有测试成绩统计如下表:
分数段 | 频数 | 频率 |
| 6 | 0.03 |
|
| 0.38 |
| 100 | 0.5 |
|
|
|
| 6 | 0.03 |
合计 | 200 | 1 |
(1)计算![]() 的值;
的值;
(2)现利用分层抽样的方法从进入决赛的学生中选择6人,再从选出的6人中选2人做进一步的研究,求选择的2人中至少有1人的分数在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com