
 +b(x≠0),其中a、b为实常数.
+b(x≠0),其中a、b为实常数. ,2],不等式f(x)≤10在x∈[
,2],不等式f(x)≤10在x∈[ ,1]上恒成立,求实数b的取值范围.
,1]上恒成立,求实数b的取值范围. +b=3x+1有且仅有一个解x=2,
+b=3x+1有且仅有一个解x=2,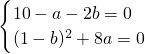 ,…解得a=-8,b=9.
,…解得a=-8,b=9. )上是减函数,在(
)上是减函数,在( ,+∞)上是增函数.
,+∞)上是增函数. ,+∞),且x1<x2,
,+∞),且x1<x2,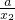 -x1-
-x1-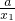 =(x2-x1)•
=(x2-x1)•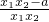 ,
, ,+∞),且x1<x2,
,+∞),且x1<x2, ,+∞)上是增函数.
,+∞)上是增函数. ,1]时有f(x)max≤10,
,1]时有f(x)max≤10, ,1]的最大值为f(
,1]的最大值为f( )与f(1)中的较大者.
)与f(1)中的较大者. ,2],不等式f(x)≤10在x∈[
,2],不等式f(x)≤10在x∈[ ,1]上恒成立,当且仅当
,1]上恒成立,当且仅当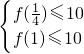 ,
,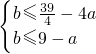 对任意的a∈[
对任意的a∈[ ,2]成立.
,2]成立. .
.  ].
]. 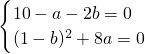 即可解得a、b的值;
即可解得a、b的值; )上是减函数,在(
)上是减函数,在( ,+∞)上是增函数;利用定义证明时,先设x1,x2∈(
,+∞)上是增函数;利用定义证明时,先设x1,x2∈( ,+∞),且x1<x2,再作差f(x2)-f(x1)后化积讨论即可;
,+∞),且x1<x2,再作差f(x2)-f(x1)后化积讨论即可;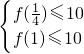 ,可解得到b≤
,可解得到b≤ ,从而可得实数b的取值范围.
,从而可得实数b的取值范围.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| f′(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中数学 来源:上海模拟 题型:解答题
| x |
| a |
| b |
| x |
| 4c2 |
| k(k+c) |
查看答案和解析>>
科目:高中数学 来源:深圳一模 题型:解答题
| 1 |
| 3 |
| f′(x) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com