
分析 设圆上任一点为P(ρ,θ),A(6,$\frac{π}{6}$),则OP=ρ,∠POA=θ-$\frac{π}{6}$,OA=2×3=6,Rt△OAP中,由OP=OAcos∠POA,化简可得圆的极坐标方程.
解答 解:设圆上任一点为P(ρ,θ),A(6,$\frac{π}{6}$),则OP=ρ,∠POA=θ-$\frac{π}{6}$,OA=2×3=6,
Rt△OAP中,OP=OAcos∠POA,ρ=6cos(θ-$\frac{π}{6}$),
而点O(0,$\frac{2}{3}$π),A(6,$\frac{π}{6}$) 符合,
故所求圆的极坐标方程为ρ=6cos(θ-$\frac{π}{6}$).
故答案为:ρ=6cos(θ-$\frac{π}{6}$).
点评 本题考查求圆的极坐标方程的方法,判断OP=ρ,∠POA=θ-$\frac{π}{6}$,OA=2×3=6,是解题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
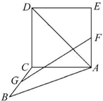 如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.
如图,正方形ACDE与等腰直角三角形ACB所在的平面互相垂直,且AC=BC=2,∠ACB=90°,F,G分别是线段AE,BC的中点,则AD与GF所成的角的余弦值为$\frac{\sqrt{3}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.
为了解沈阳市高三学生某次模拟考试的数学成绩的某项指标,从所有成绩在及格线以上(90及90分以上)的考生中抽取一部分考生对其成绩进行统计,将成绩按如下方式分成六组,第一组[90,100)、第二组[100,110)…第六组[140,150].如图为其频率分布直方图的一部分,若第四、五、六组的人数依次成等差数列,且第六组有4人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com