
【题目】关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最大值为
的最大值为![]() ;
;
③![]() 在
在![]() 有
有![]() 个零点;④
个零点;④![]() 在区间
在区间![]() 单调递增.
单调递增.
其中所有正确结论的编号是( )
A.①②B.①③C.②④D.①④
【答案】D
【解析】
利用偶函数的定义可判断出命题①的正误;分![]() 和
和![]() 两种情况,去绝对值,利用辅助角公式以及正弦函数的最值可判断命题②的正误;分
两种情况,去绝对值,利用辅助角公式以及正弦函数的最值可判断命题②的正误;分![]() 和
和![]() 两种情况讨论,求出函数
两种情况讨论,求出函数![]() 的零点,可判断命题③的正误;去绝对值,将函数
的零点,可判断命题③的正误;去绝对值,将函数![]() 的解析式化简,结合正弦型函数的单调性可判断出命题④的正误.
的解析式化简,结合正弦型函数的单调性可判断出命题④的正误.
对于命题①,函数![]() 的定义域为
的定义域为![]() ,关于原点对称,且
,关于原点对称,且![]()
![]() ,该函数的为偶函数,命题①正确;
,该函数的为偶函数,命题①正确;
对于命题②,当函数![]() 取最大值时,
取最大值时,![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,
此时,![]() ,当
,当![]() ,函数
,函数![]() 取得最大值
取得最大值![]() .
.
当![]() 时,
时,![]() ,
,
此时,![]() ,当
,当![]() ,函数
,函数![]() 取得最大值
取得最大值![]() .
.
所以,函数![]() 的最大值为
的最大值为![]() ,命题②错误;
,命题②错误;
对于命题③,当![]() 时,令
时,令![]() ,则
,则![]() ,此时
,此时![]() ;
;
当![]() 时,令
时,令![]() ,则
,则![]() ,此时
,此时![]() .
.
所以,函数![]() 在区间
在区间![]() 上有且只有两个零点,命题③错误;
上有且只有两个零点,命题③错误;
对于命题④,当![]() 时,
时,![]() ,则
,则![]() .
.
所以,函数![]() 在区间
在区间![]() 上单调递增,命题④错误.
上单调递增,命题④错误.
因此,正确的命题序号为①④.
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
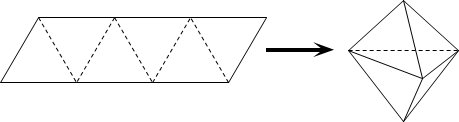
【题目】农历五月初五是端午节,民间有吃粽子的习惯,粽子又称粽籺,俗称“粽子”,古称“角黍”,是端午节大家都会品尝的食品,传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图,平行四边形形状的纸片是由六个边长为1的正三角形构成的,将它沿虚线折起来,可以得到如图所示粽子形状的六面体,则该六面体的体积为____;若该六面体内有一球,则该球体积的最大值为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是无穷数列.给出两个性质:
是无穷数列.给出两个性质:
①对于![]() 中任意两项
中任意两项![]() ,在
,在![]() 中都存在一项
中都存在一项![]() ,使
,使![]() ;
;
②对于![]() 中任意项
中任意项![]() ,在
,在![]() 中都存在两项
中都存在两项![]() .使得
.使得![]() .
.
(Ⅰ)若![]() ,判断数列
,判断数列![]() 是否满足性质①,说明理由;
是否满足性质①,说明理由;
(Ⅱ)若![]() ,判断数列
,判断数列![]() 是否同时满足性质①和性质②,说明理由;
是否同时满足性质①和性质②,说明理由;
(Ⅲ)若![]() 是递增数列,且同时满足性质①和性质②,证明:
是递增数列,且同时满足性质①和性质②,证明:![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应绿色出行,某市推出了新能源分时租赁汽车,并对该市市民使用新能源租赁汽车的态度进行调查,得到有关数据如下表1:
表1
愿意使用新能源租赁汽车 | 不愿意使用新能源租赁汽车 | 总计 | |
男性 | 100 | 300 | |
女性 | 400 | ||
总计 | 400 |
其中一款新能源分时租赁汽车的每次租车费用由行驶里程和用车时间两部分构成:行驶里程按1元/公里计费;用车时间不超过30分钟时,按0.15元/分钟计费;超过30分钟时,超出部分按0.20元/分钟计费.已知张先生从家到上班地点15公里,每天上班租用该款汽车一次,每次的用车时间均在20~60分钟之间,由于堵车红绿灯等因素,每次的用车时间![]() (分钟)是一个随机变量.张先生记录了100次的上班用车时间,并统计出在不同时间段内的频数如下表2:
(分钟)是一个随机变量.张先生记录了100次的上班用车时间,并统计出在不同时间段内的频数如下表2:
表2
时间 | (20,30] | (30,40] | (40,50] | (50,60] |
频数 | 20 | 40 | 30 | 10 |
(1)请补填表1中的空缺数据,并判断是否有99.5%的把握认为该市市民对新能源租赁汽车的使用态度与性别有关;
(2)根据表2中的数据,将各时间段发生的频率视为概率,以各时间段的区间中点值代表该时间段的取值,试估计张先生租用一次该款汽车上班的平均用车时间;
附: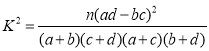
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数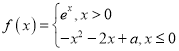 ,则下列说法正确的是( )
,则下列说法正确的是( )
A.若![]() ,则
,则![]() 的图象上存在唯一一对关于原点
的图象上存在唯一一对关于原点![]() 对称的点
对称的点
B.存在实数![]() 使得
使得![]() 的图象上存在两对关于原点
的图象上存在两对关于原点![]() 对称的点
对称的点
C.不存在实数![]() 使得
使得![]() 的图象上存在两对关于
的图象上存在两对关于![]() 轴对称的点
轴对称的点
D.若![]() 的图象上存在关于
的图象上存在关于![]() 轴对称的点,则
轴对称的点,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,则
,则![]() 的坐标为_____________,直线
的坐标为_____________,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的重心恰为点
的重心恰为点![]() ,则直线
,则直线![]() 斜率为_____________.
斜率为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》有这样一个问题:从冬至日起,依次小寒、大寒、立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种十二个节气日影长减等寸,雨水、惊蛰、春分、清明日影之和为三丈二尺,前七个节气日影之和为七丈三尺五寸,问立夏日影长为( )
A.七尺五寸B.六尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体![]() 中,P为线段
中,P为线段![]() 上的动点,下列说法正确的是( )
上的动点,下列说法正确的是( )
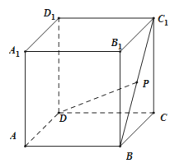
A.对任意点P,![]() 平面
平面![]()
B.三棱锥![]() 的体积为
的体积为![]()
C.线段DP长度的最小值为![]()
D.存在点P,使得DP与平面![]() 所成角的大小为
所成角的大小为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,
,![]() 、
、![]() 分别为椭圆长轴的左、右端点,
分别为椭圆长轴的左、右端点,![]() 为直线
为直线![]() 上异于点
上异于点![]() 的任意一点,连接
的任意一点,连接![]() 交椭圆于
交椭圆于![]() 点.
点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)是否存在![]() 轴上的定点
轴上的定点![]() 使得以
使得以![]() 为直径的圆恒过
为直径的圆恒过![]() 与
与![]() 的交点?如果存在,请求出定点
的交点?如果存在,请求出定点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com