
����Ŀ��Ϊ���о���ͬ�Ա��ڴ���������ʱ�ı��ֲ��죬�ټ�����Ů־Ը�߸�200����Ҫ������ͬʱ��ɶ�����������⡢����ͼ���ӵ绰.��ͼ��ʾ��־Ը��������������ʱ��ֲ�.���½��ۣ���־Ը��������������ʱ��ֲ�ͼ��������ȷ���ǣ� ��

�����忴Ů�Դ���������ƽ����ʱ���̣�
������Ů�Դ����������������Ҫ�������ԣ�
�����Ե�ʱ��ֲ����ӽ���̬�ֲ���
��Ů�Դ������������ʱΪ���������Դ������������ʱΪ����.
A.�٢�B.�ڢ�C.�٢�D.�ڢ�
���𰸡�C
��������
ͼ��Ϊ��־Ը��������������ʱ��ֲ�ͼ��,����ͼ�����η�������
��ͼ,Ů�Դ�����������ʱ��Ҫ������2��3����,���Դ�����������ʱ��Ҫ������3��4����,����������Ů�Դ�����������ʱ����,�ʢ���ȷ��
Ů����Ҳ�д�����������ʱ��5���ӵ�,����������Ů�Դ���������������Ҫ��������,�ʢڴ���
��ͼ�����������Ե�ʱ��ֲ����ӽ���̬�ֲ�,�ʢ���ȷ��
���ԡ�Ů�Դ������������ʱ��Ϊ����,�ʢܴ���
����,�٢���ȷ,
��ѡ:C


 ���Ž�������С״Ԫϵ�д�
���Ž�������С״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ԲO��x2+y2��3�ϵ�һ����M��x���ϵ�ͶӰΪN����P����![]() ��
��
��1����P�Ĺ켣C�ķ��̣�
��2����ֱ��l��ԲO���У��ҽ�����C�ڵ�A��B������|AB|�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�a��b��c�ֱ��ǽ�A��B��C�ĶԱߣ���acosC����2b��c��cosA.
��1����![]() 3�����ABC�������
3�����ABC�������
��2������B����C����2cos2B+cos2C��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�Ϊ��ABC�����ڽ�A��B��C�ĶԱߣ���acos C��![]() asin C��b��c��0.
asin C��b��c��0.
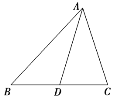
(1)��A��
(2)��ADΪBC���ϵ����ߣ�cos B��![]() ��AD��
��AD��![]() �����ABC�������
�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������ԭ��
�У�������ԭ��![]() Ϊ���㣬
Ϊ���㣬![]() ���������Ϊ���Ὠ��������ϵ������
���������Ϊ���Ὠ��������ϵ������![]() �ķ���Ϊ
�ķ���Ϊ![]() ������
������![]() ��ֱ��
��ֱ��![]() �IJ�������Ϊ
�IJ�������Ϊ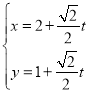 ��
��![]() ������.
������.
������ֱ��![]() ����ͨ����������
����ͨ����������![]() ��ֱ�����귽�̣�
��ֱ�����귽�̣�
������ֱ��![]() ������
������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() ��ֵ������
��ֵ������![]() ��
��![]() ��
��![]() ����ľ���֮��.
����ľ���֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������T�Ľ���ΪF����Ϊl����F��ֱ��m��T����A��B���㣬C��D�ֱ�ΪA��B��l�ϵ���Ӱ��MΪAB���е㣬��m��l��ƽ�У����CMD��(����)
A. ���������������������
B. ������������Ϊ�۽�������
C. ����ֱ��������
D. �ǵ�����ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() .
.
��1��������![]() ��ͼ����
��ͼ����![]() ����������
����������![]() ��ƽ�У���
��ƽ�У���![]() ��ֵ��
��ֵ��
��2����![]() ʱ��
ʱ��![]() ���������
���������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() �����߷���Ϊ
�����߷���Ϊ![]() ��
��![]() ��
��![]() �ֱ�����Բ
�ֱ�����Բ![]() �����Ҷ��㣬���ҽ���
�����Ҷ��㣬���ҽ���![]() ��б��Ϊ
��б��Ϊ![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ����.
����.
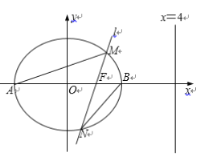
��1������Բ![]() �ı�����.
�ı�����.
��2����![]() ��
��![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ��
��![]() ����
����![]() ����
����![]() ��ֵ��
��ֵ��
��3�����߶�![]() ���е�Ϊ
���е�Ϊ![]() ��ֱ��
��ֱ��![]() �������ཻ�ڵ�
�������ཻ�ڵ�![]() ����ֱ��
����ֱ��![]() ��
��![]() ��
��![]() ��б�ʷֱ�Ϊ
��б�ʷֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��������Ϊ
��������Ϊ![]() ��M����ԲC���϶��㣬
��M����ԲC���϶��㣬![]() ��F2����ԲC�Ľ��㣬
��F2����ԲC�Ľ��㣬![]() ���ܳ���6��
���ܳ���6��
��������ԲC�ı����̣�
��������P��1��t����ֱ�߽���ԲC��A��B���㣬��|PA|=|PB|����P��ֱ��l��ʹl��ֱ��AB��ֱ��֤����ֱ��l������㣬����˶�������꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com