
 (a〉b>0)的左焦点为
(a〉b>0)的左焦点为 ,椭圆过点P(
,椭圆过点P(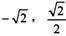 )
)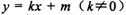 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.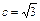 ,b2 = a2-3,由
,b2 = a2-3,由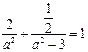 得 2a4-11a2 + 12 = 0,
得 2a4-11a2 + 12 = 0,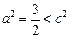 (舍去),
(舍去),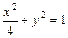 . ……………… 4分
. ……………… 4分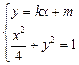 得
得 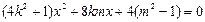 .
.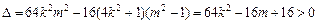 ,
,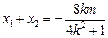 ,
,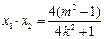 ,
,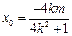 ,
,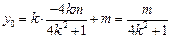 ,
,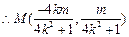 .
.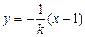 ,则有 x =-ky + 1.
,则有 x =-ky + 1.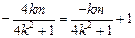 ,所以
,所以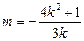 . ②
. ②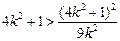 ,
, 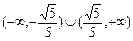 . ……………… 12分
. ……………… 12分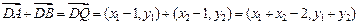
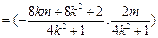
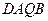 对角线互相垂直,即直线l与
对角线互相垂直,即直线l与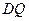 垂直,由斜率的负倒数关系可整理得
垂直,由斜率的负倒数关系可整理得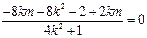 ,即-3km = 4k2 + 1,即
,即-3km = 4k2 + 1,即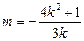 , 代入①即得.
, 代入①即得.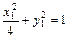 ,
, ,于是,两式相减可得
,于是,两式相减可得 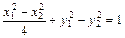 ,
,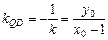 . ②
. ②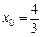 ,
,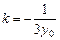 ,表明点M的轨迹为线段
,表明点M的轨迹为线段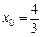 (
(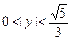 ).
).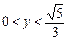 ,k∈(
,k∈(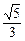 ,+∞);当
,+∞);当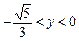 ,k∈(-∞,
,k∈(-∞,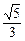 ).
).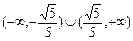 .
.

科目:高中数学 来源:不详 题型:解答题

 在直线
在直线 上。
上。 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
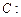
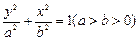 经过点
经过点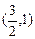 ,一个焦点是
,一个焦点是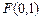 .
.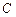 的方程;
的方程;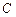 与
与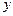 轴的两个交点为
轴的两个交点为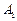 、
、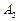 ,不在
,不在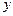 轴上的动点
轴上的动点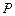 在直线
在直线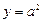 上运动,直线
上运动,直线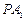 、
、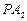 分别与椭圆
分别与椭圆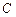 交于点
交于点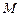 、
、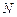 ,证明:直线
,证明:直线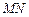 经过焦点
经过焦点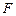 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com