
分析 (Ⅰ)在定义域内解不等式F′(x)>0,F′(x)<0可得函数的单调区间;
(Ⅱ)(i)根据函数的单调区间,得到$F(x)≥F(\sqrt{e})$,从而证出结论;
(ii)由(I)可知,当x=$\sqrt{e}$时,F(x)取得最小值F($\sqrt{e}$)=0,则f(x)与g(x)的图象在x=$\sqrt{e}$处有公共点($\sqrt{e}$,$\frac{e}{2}$).假设f(x)与g(x)存在“分界线”,则其必过点($\sqrt{e}$,$\frac{e}{2}$).故设其方程为:y-$\frac{e}{2}$=k(x-$\sqrt{e}$),由f(x)≥kx+$\frac{e}{2}$-k$\sqrt{e}$对x∈R恒成立,可求得k=$\sqrt{e}$,则“分界线“的方程为:y=$\sqrt{e}$x-$\frac{e}{2}$.只需在证明g(x)≤$\sqrt{e}$x-$\frac{e}{2}$对x∈(0,+∞)恒成立即可.
解答 解:(I)由于函数f(x)=$\frac{1}{2}$x2,g(x)=elnx,
因此,F(x)=f(x)-g(x)=$\frac{1}{2}$x2-elnx,
则F′(x)=x-$\frac{e}{x}$=$\frac{{x}^{2}-e}{x}$=$\frac{(x-\sqrt{e})(x+\sqrt{e})}{x}$,x∈(0,+∞),
当0<x<$\sqrt{e}$时,F′(x)<0,∴F(x)在(0,$\sqrt{e}$)上是减函数;
当x>$\sqrt{e}$时,F′(x)>0,∴F(x)在($\sqrt{e}$,+∞)上是增函数;
因此,函数F(x)的单调减区间是(0,$\sqrt{e}$),单调增区间是($\sqrt{e}$,+∞).
(Ⅱ)(ⅰ)证明:由(Ⅰ)得函数F(x)的单调减区间是(0,$\sqrt{e}$),单调增区间
是($\sqrt{e}$,+∞)∴$F(x)≥F(\sqrt{e})$,而$F(\sqrt{e})=\frac{1}{2}{({\sqrt{e}})^2}-eln\sqrt{e}=0$,
即F(x)≥0∴f(x)≥g(x)成立;
(II)(ii)由(I)可知,当x=$\sqrt{e}$时,F(x)取得最小值F($\sqrt{e}$)=0,
则f(x)与g(x)的图象在x=$\sqrt{e}$处有公共点($\sqrt{e}$,$\frac{e}{2}$),
假设f(x)与g(x)存在“分界线”,则其必过点($\sqrt{e}$,$\frac{e}{2}$),
故设其方程为:y-$\frac{e}{2}$=k(x-$\sqrt{e}$),即y=kx+$\frac{e}{2}$-k$\sqrt{e}$,
由f(x)≥kx+$\frac{e}{2}$-k$\sqrt{e}$对x∈R恒成立,则x2-2kx-e+2k$\sqrt{e}$≥0对x∈R恒成立,
∴△=4k2-4(2k$\sqrt{e}$-e)=4k2-8k$\sqrt{e}$+4e=e(k-$\sqrt{e}$)2≤0成立,
因此k=$\sqrt{e}$,“分界线“的方程为:y=$\sqrt{e}$x-$\frac{e}{2}$,
下面证明g(x)≤$\sqrt{e}$x-$\frac{e}{2}$对x∈(0,+∞)恒成立,
设G(x)=elnx-x$\sqrt{e}$+$\frac{e}{2}$,则G′(x)=$\frac{e}{x}$-$\sqrt{e}$=$\frac{\sqrt{e}(\sqrt{e}-x)}{x}$,
∴当0<x<$\sqrt{e}$时,G′(x)>0,当x>$\sqrt{e}$时,G′(x)<0,
当x=$\sqrt{e}$时,G(x)取得最大值0,则g(x)≤$\sqrt{e}$x-$\frac{e}{2}$对x∈(0,+∞)恒成立,
故所求“分界线“的方程为:y=$\sqrt{e}$x-$\frac{e}{2}$.
点评 本题考查利用导数研究函数的单调区间、最值及恒成立问题,考查转化思想,探究性题目往往先假设成立,再做一般性证明.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
 已知点R是圆心为Q的圆(x+$\sqrt{3}$)2+y2=16上的一个动点,N($\sqrt{3}$,0)为定点,线段RN的中垂线与直线QR交于点T,设T点的轨迹为曲线C.
已知点R是圆心为Q的圆(x+$\sqrt{3}$)2+y2=16上的一个动点,N($\sqrt{3}$,0)为定点,线段RN的中垂线与直线QR交于点T,设T点的轨迹为曲线C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
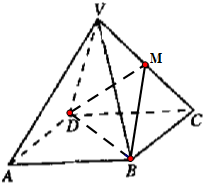 如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为$\sqrt{5}$的等腰三角形,M为VC边中点.
如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为$\sqrt{5}$的等腰三角形,M为VC边中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3} | B. | {x|1<x<3} | C. | {2,3} | D. | {x|1<x<$\sqrt{10}$} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com