
| 1 |
| an |
| 1 |
| an+1 |
| 2 |
| anan+1 |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
| (n-1)2 |
| 2 |
| 1 |
| an |
| 1 |
| an+1 |
| 2 |
| anan+1 |
| sn |
| n |
| S2 |
| 2 |
| S3 |
| 3 |
| Sn |
| n |
| (n-1)2 |
| 2 |
| n(n+1) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| ex |
| a |
| a |
| ex |
查看答案和解析>>
科目:高中数学 来源: 题型:
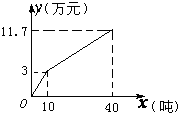 春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.如图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题:
春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.如图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题:查看答案和解析>>
科目:高中数学 来源: 题型:
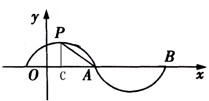 已知函数f(x)=sin[ωπ(x+
已知函数f(x)=sin[ωπ(x+| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,求它落在扇形外正方形内的概率.
如图,在正方形内有一扇形(见阴影部分),扇形对应的圆心是正方形的一顶点,半径为正方形的边长.在这个图形上随机撒一粒黄豆,求它落在扇形外正方形内的概率.查看答案和解析>>
科目:高中数学 来源: 题型:
| a(x2-1) |
| x(a2-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com