

分析 (1)画树状图能写出两次摸牌出现的所有可能的结果.
(2)共有12种等可能的结果数,能判断四边形ABCD为平行四边形有6种,由此能求出能判断四边形ABCD为平行四边形的概率.
解答 解:(1)画树状图为: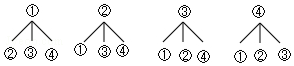
∴两次摸牌出现的所有可能的结果为:
①②,①③,①④,②①,②③,②④,③①,③②,③④,④①,④②,④③.
(2)共有12种等可能的结果数,
其中能判断四边形ABCD为平行四边形有6种:
①③、①④、②③、③①、③②、④①,
所以能判断四边形ABCD为平行四边形的概率p=$\frac{6}{12}$=$\frac{1}{2}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | 2 | C. | $\frac{8}{3}$ | D. | $\frac{{16\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | (-∞,-$\frac{1}{2}$] | C. | (-∞,-$\frac{1}{2}$]∪(-$\frac{1}{2}$,0] | D. | (-$\frac{1}{2}$,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0) | B. | (0,3) | C. | (-∞,-1]∪[3,+∞) | D. | (-∞,0]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com