
(本小题满分12分)已知向量 设函数
设函数
(1)求 的最小正周期与单调递减区间;
的最小正周期与单调递减区间;
(2)在 中
中 、
、 、
、 分别是角
分别是角 的对边,若
的对边,若
 的面积为
的面积为 ,求
,求 的值.
的值.
科目:高中数学 来源: 题型:解答题
(本题满分16分)
(提示:1、12、13、14班同学请完成试题(B),其他班级同学任选试题(A)或(B)作答)
(A) 已知点A(2,3),B(5,4),C(7,10)及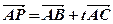 ,试问:
,试问:
(1)t为何值时,P在第三象限?
(2)是否存在D点使得四边形ABCD为平行四边形,若存在,求出D点坐标.
(B) 已知平行四边形ABCD,对角线AC与BD交于点E,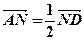 ,连接BN交AC于M,
,连接BN交AC于M,
(1)若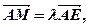 求实数λ.
求实数λ.
(2)若B(0,0),C(1,0),D(2,1),求M的坐标
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
如图,在 中,设
中,设 ,
, ,
, 的中点为
的中点为 ,
, 的中点为
的中点为 ,
, 的中点恰为
的中点恰为 .
.
(Ⅰ)若 ,求
,求 和
和 的值;
的值;
(Ⅱ)以 ,
, 为邻边,
为邻边,  为对角线,作平行四边形
为对角线,作平行四边形 ,
,
求平行四边形 和三角形
和三角形 的面积之比
的面积之比 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com