练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，已知椭圆 与双曲线 有相同的焦点，且椭圆 过点 ，若直线 与直线 平行且与椭圆 相交于点 ,B(x2,y2)．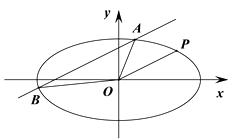

    (Ⅰ) 求椭圆的标准方程；
    (Ⅱ) 求三角形 面积的最大值.

    【答案】解：(Ⅰ)由已知有 ，∴

    ∴椭圆 的标准方程为 .

    (Ⅱ)∵ ,∴设直线 方程为

    代入 得：

    ∴当 ，即 时，设 ，则： ,

    ∴

    （当且仅当 时，取等号）

    ∴ 的最大值为 .


    【解析】(1)由椭圆过已知点及与已知双曲线有相同焦点，可得到关于a,b,c的方程组，求a,b,c得到椅子圆方程。
    （2）将直线方程代入椭圆方程得到关于x的一元二次方程，由韦达定理和弦长公式将三角形面积表示为m的函数式，求最大值。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设函数f（x）在R上存在导数f′（x），x∈R，有f（﹣x）+f（x）=x2 ， 在（0，+∞）上f′（x）＜x，若f（4﹣m）﹣f（m）≥8﹣4m．则实数m的取值范围为（ ）
    A.[﹣2，2]
    B.[2，+∞）
    C.[0，+∞）
    D.（﹣∞，﹣2]∪[2，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 （a＞0）． （Ⅰ）当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；
    （Ⅱ）若 恒成立，求a的取值范围；
    （Ⅲ）证明：总存在x0 ， 使得当x∈（x0 ， +∞），恒有f（x）＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥P﹣ABCD中，底面ABCD是∠DAB=60°且边长为a的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD，若G为AD边的中点，
    （1）求证：BG⊥平面PAD；
    （2）求证：AD⊥PB；
    （3）若E为BC边的中点，能否在棱PC上找到一点F，使平面DEF⊥平面ABCD，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 的两个零点 满足 ，集合 ，则（ ）
    A.m∈A ， 都有f(m＋3)>0
    B.m∈A ， 都有f(m＋3)<0
    C.m0∈A ， 使得f(m0＋3)＝0
    D.m0∈A ， 使得f(m0＋3)<0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在边长为2的正六边形ABCDEF中，动圆Q的半径为1，圆心在线段CD（含端点）上运动，P是圆Q上及内部的动点，设向量 （m，n为实数），则m+n的取值范围是（　　）

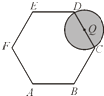
    A.（1，2]
    B.[5，6]
    C.[2，5]
    D.[3，5]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知曲线C的极坐标方程是ρ=2，以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为 （t为参数）．
    （Ⅰ）写出直线l的普通方程与曲线C的直角坐标方程；
    （Ⅱ）设曲线C经过伸缩变换 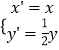得到曲线C'，若点P（1，0），直线l与C'交与A，B，求|PA||PB|，|PA|+|PB|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C的中心在坐标原点，焦点在x轴上，左顶点为A，左焦点为F1（﹣2，0），点B（2， ）在椭圆C上，直线y=kx（k≠0）与椭圆C交于E，F两点，直线AE，AF分别与y轴交于点M，N
    （Ⅰ）求椭圆C的方程；
    （Ⅱ）在x轴上是否存在点P，使得无论非零实数k怎样变化，总有∠MPN为直角？若存在，求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}为递增的等差数列，a1=f（x+1），a2=0，a3=f（x﹣1），其中f（x）=x2﹣4x+2，则数列{an}的通项公式为（ ）
    A.an=n﹣2
    B.an=2n﹣4
    C.an=3n﹣6
    D.an=4n﹣8

    查看答案和解析>>

    同步练习册答案