
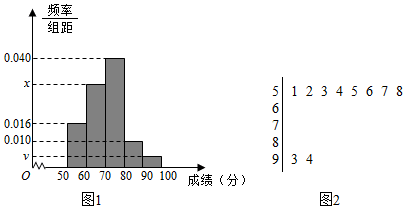
分析 (1)由频率公式和图求出样本容量n,由频率分布直方图中的数据求出x、y的值;
(2)先求出分数在[80,90)、[90,100]内的学生人数,求出抽取的3名学生中得分在[80,90)的人数X的可能取值,由概率公式分别求出它们的概率并列出X的分布列,代入公式求出EX.
(3)由排列组合知识可求得.
解答 解:(1)由题意可知,样本容量$n=\frac{8}{0.016×10}=50$,$y=\frac{2}{50×10}=0.004$,x=0.100-0.004-0.010-0.016-0.040=0.030.
(2)由题意可知,分数在[80,90)内的学生有5人,分数在[90,100]内的学生有2人,共7人.抽取的3名学生中得分在[80,90)的人数X的可能取值为1,2,3,则$P(X=1)=\frac{C_5^1C_2^2}{C_7^3}=\frac{5}{35}=\frac{1}{7}$,$P(X=2)=\frac{C_5^2C_2^1}{C_7^3}=\frac{20}{35}=\frac{4}{7}$,$P(X=3)=\frac{C_5^3C_2^0}{C_7^3}=\frac{10}{35}=\frac{2}{7}$.
| X | 1 | 2 | 3 |
| P | $\frac{1}{7}$ | $\frac{4}{7}$ | $\frac{2}{7}$ |
点评 本题考查茎叶图、频率分布直方图,考查随机了的分布列及其数学期望,考查学生的识图能力,考查学生的计算能力,属于中档题


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com