
分析 (Ⅰ)由cos2t+sin2t=1,消去t,化简整理,可得曲线C的直角坐标方程;
(Ⅱ)解法一、求得直线方程y=x,设与直线l平行的直线方程为y=x+m,代入曲线方程,运用判别式为0,可得m的值,由平行直线的距离公式可得最大值;
解法二、设点P(3cost,2+2sint),运用点到直线的距离公式和辅助角公式,结合正弦函数的值域,即可得到所求最大值.
解答 解:(Ⅰ)由x=3cost,y=2+2sint,且cos2t+sin2t=1,
消去参数t,得曲线C的直角坐标方程为$\frac{x^2}{9}+\frac{{{{({y-2})}^2}}}{4}=1$.
(Ⅱ)解法一、直线l的直角坐标方程为y=x.
设与直线l平行的直线方程为y=x+m,代入$\frac{x^2}{9}+\frac{{{{({y-2})}^2}}}{4}=1$,
整理得13x2+18(m-2)x+9[(m-2)2-4]=0.
由△=[18(m-2)]2-4×13×9[(m-2)2-4]=0,得(m-2)2=13,
所以$m=2±\sqrt{13}$.
当点P位于直线$y=x+2+\sqrt{13}$与曲线C的交点(切点)时,
点P到直线l的距离最大,为$\frac{{2+\sqrt{13}}}{{\sqrt{2}}}=\frac{{2\sqrt{2}+\sqrt{26}}}{2}$.
解法二、设点P(3cost,2+2sint),
则点P到直线x-y=0的距离为$\frac{{|{3cost-2-2sint}|}}{{\sqrt{2}}}=\frac{{|{\sqrt{13}sin({t-φ})+2}|}}{{\sqrt{2}}}$,
其中$cosφ=\frac{2}{{\sqrt{13}}},sinφ=\frac{3}{{\sqrt{13}}}$.
所以距离的最大值是$\frac{{\sqrt{13}+2}}{{\sqrt{2}}}=\frac{{2\sqrt{2}+\sqrt{26}}}{2}$.
点评 本题考查参数方程与直角坐标方程的互化,注意运用同角的平方关系,考查点到直线的距离的最大值,注意运用参数方程和点到直线的距离公式,以及联立直线和曲线方程,运用判别式为0,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
 如图,边长为2的正方形ABCD中,BE=BF=$\frac{1}{4}$BC,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于A′点,则三棱锥A′-EFD的体积为( )
如图,边长为2的正方形ABCD中,BE=BF=$\frac{1}{4}$BC,将△AED,△DCF分别沿DE,DF折起,使A,C两点重合于A′点,则三棱锥A′-EFD的体积为( )| A. | $\frac{{\sqrt{21}}}{12}$ | B. | $\frac{{\sqrt{17}}}{12}$ | C. | $\frac{{\sqrt{21}}}{6}$ | D. | $\frac{{\sqrt{17}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,10) | B. | (-2,10] | C. | [6,10] | D. | (6,10] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
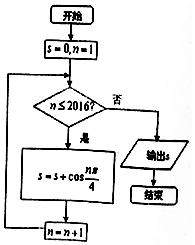
| A. | 0 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$+1 | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 5 | C. | 10 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {1,2,3} | C. | {0,1,2} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人数 | 10 | 20 | 40 | 20 | 10 |
| 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(k2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.076 | 3.84 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com