
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
分析 不妨设P在右支上,由双曲线的定义可得PF1-PF2=2a,再由条件分别求得△PF1F2三边长,运用三角形的海伦面积公式,结合离心率公式,解方程即可得到所求值.
解答 解:不妨设P在右支上,则PF1-PF2=2a,
又PF1+PF2+F1F2=6c,即PF1+PF2=4c,
解得PF1=a+2c,PF2=2c-a,
由海伦面积公式可得,△PF1F2的面积为
S△=$\sqrt{3c(3c-2c)(3c-a-2c)(3c-2c+a)}$=$\sqrt{3{c}^{2}({c}^{2}-{a}^{2})}$,
由题意可得$\frac{2\sqrt{3}}{3}$a2=$\sqrt{3{c}^{2}({c}^{2}-{a}^{2})}$,
两边平方可得,9c4-9a2c2-4a4=0,
由e=$\frac{c}{a}$,可得,9e4-9e2-4=0,
解得e2=$\frac{4}{3}$,即有e=$\frac{2\sqrt{3}}{3}$.
故选A.
点评 本题考查双曲线的定义、方程和性质,主要考查离心率的求法,同时考查三角形的面积公式的运用,属于中档题..


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
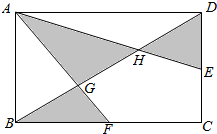 如图:长方体ABCD中,AB=10厘米,BC=15厘米,E,F分别是所在边的中点,求阴影部分的面积.(提示:由于图中AD平行于BC,可知AD:BF=AG:CF=DG:BG)
如图:长方体ABCD中,AB=10厘米,BC=15厘米,E,F分别是所在边的中点,求阴影部分的面积.(提示:由于图中AD平行于BC,可知AD:BF=AG:CF=DG:BG)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S正<S球<S柱 | B. | S正<S柱<S球 | C. | S球<S柱<S正 | D. | S球<S正<S柱 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
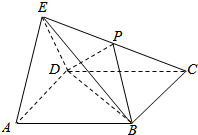 如图,在四棱锥E-ABCD中,底面ABCD为正方形,侧面EAD是正三角形,平面EAD⊥平面ABCD为正方形,P为EC的中点.
如图,在四棱锥E-ABCD中,底面ABCD为正方形,侧面EAD是正三角形,平面EAD⊥平面ABCD为正方形,P为EC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
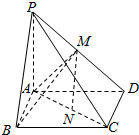 已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.
已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com