ñøö—ȤȴÂþÈˋÈ´iÈˋ꘧ÃOÀðMȘÆèØîøˆä¾¥±ëó祰—OÀðMÀëó§ûÌAAÀðBÀðBȘONÀëó§ûÌAAÀðBÀðBȘùªØåOÀðMÀöONȘÆèÇùáÉøÊû¼OMÀöó§ûÌAAÀðBÀðBÈÛ
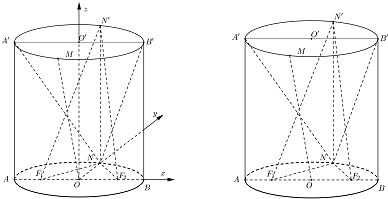
È´iiÈˋØåOöˆåÙçÐȘABùªåÖøÝüÔöˆxøÃȘOOÀðùªåÖøÝüÔöˆzøÃȘ§´ê¢í¥ðøݧúæ½ÝõüçȘâ«Æûü·ê¢ñ´áÉúµ°—ó§ûÌABNÆŠó§ûÌAÀðBÀðNùª°èàþѱû̧úçáÆÁüØøçÈÛ
ȴ·ÈˋçÝçÐNöˆüôçæûÌèüëøåýçáÑäøÃÑùçÐòÝȘtanÈ´Îê+ÎôÈˋ=-
È£çÝçÐNöˆüôçæûÌèüëøåýçá°ÊøÃÑùçÐÈ´àÓÆØÑËçÐÈˋòÝȘ
tan(Îê+Îô)=-ȘøÝ¿ÜéÅÑütanÈ´Îê+ÎôÈˋçáàÀøçñÑöÏòú[-
Ș-
]ÈÛÆèØîøˆä¾¥±ëó祰—
ÀüNÀðF1NȘÀüNÀðF2NñøÝÞöˆNÀðF
1ȘNÀðF
2ÆŠüôçæûÌùª°èçá§úȘ
ÀüNÀðF1N=ÎêȘÀüNÀðF2N=ÎôȘÆèÇùáÉøÊû¼tanÈ´Îê+ÎôÈˋçáàÀøçñÑöÏòú[-
Ș-
]ÈÛ
§ãÇÞȤ
È´ÂþÈˋÈ´iÈˋøÊû¼È¤ê˜§ÃOÀðMȘOÀðNȘÀÔOÀðOÀëçæûÌAÀðBÀðNÀðȘOÀðM?çæûÌAÀðBÀðNÀðȘ
ÀÁOÀÛOÀëOÀðMȘÀÔOÀðMÀëAÀðBÀðȘOÀðO?ó§ûÌAAÀðBÀðBȘAÀðBÀð?ó§ûÌAAÀðBÀðBȘAÀðBÀðÀèOÀðO=OÀðȘ
ÀÁOÀðMÀëó§ûÌAAÀðBÀðBȘë˜âÚONÀëó§ûÌAAÀðBÀðBȘÀÁOÀðMÀöONȘ
ÆøOÀðM=ONȘÀÁùáÝÔÅöONOÀðMöˆó§ÅÅùáÝÔÅöȘ
ÆøÀÔOMý£¯■¤˜ÆÖó§ûÌAAÀðBÀðBȘOÀðN?ó§ûÌAAÀðBÀðBȘ
ÀÁOMÀöó§ûÌAAÀðBÀðBÈÛ
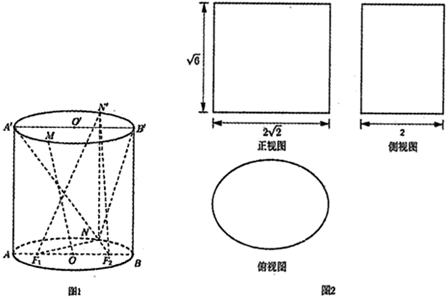
È´iiÈˋ§ãȤÆèäãØãçû
AAÀð=ȘçæûÌèüçáëøåýçá°ÊøðÊ2
ȘÑäøðÊöˆ2Ș
àÓë¥È˜ØåOöˆåÙçÐȘABùªåÖøÝüÔöˆxøÃȘOOÀðùªåÖøÝüÔöˆzøÃȘ
§´ê¢í¥ðøݧúæ½ÝõüçȘ
å·ÆÅF
2È´1Ș0Ș0ÈˋȘNÈ´0Ș1Ș0ÈˋȘ
AÀð(-Ș0Ș)Ș
BÀð(Ș0Ș)Ș
=(-Ș-1Ș)Ș=(Ș0Ș)Ș
ÀÁ
=È´0
Ș-1ȘÈˋȘ
=(Ș-1Ș)Ș
ÀÔzøÃÀëó§ûÌABNȘÀÁàÀó§ûÌABNçáØ£¡—ñ´ü·ê¢
=(0Ș0Ș1)Ș
èÒó§ûÌAÀðBÀðNçáØ£¡—ñ´ü·ê¢öˆ
=(xȘyȘz)Ș
å·
ȘàÀz=1Șçû
=(0ȘȘ1)Ș
èÒó§ûÌABNÆŠó§ûÌAÀðBÀðNùª°èàþѱû̧úçáó§û̧úöˆÎàȘ
å·cosÎà=|cosÈ¥
Șȃ|=|
|=
Ș
ÀÁó§ûÌABNÆŠó§ûÌAÀðBÀðNùª°èàþѱû̧úçáÆÁüØøçöˆ
ÈÛ
ȴ·Èˋ§ãȤçÝçÐNöˆüôçæûÌèüëøåýçáÑäøÃÑùçÐòÝȘ
NF1=NF2=ȘtanÎê=tanÎô=
=
=
Ș
Îê=Îô=Ș
Îê+Îô=ȘtanÈ´Îê+ÎôÈˋ=-
È£
çÝçÐNöˆüôçæûÌèüëøåýçá°ÊøÃÑùçÐÈ´àÓÆØÑËçÐÈˋòÝȘ
NF
1=
+1ȘNF
2=
-1Ș
tanÎê=
=Ștan
Îô==
Ș
tan(Îê+Îô)=-Ș
øÝ¿ÜéÅÑütanÈ´Îê+ÎôÈˋçáàÀøçñÑöÏòú[-
Ș-
]Ș
ÀÔNÀðòúçÐNåÖèüçæûÌçáëÑƯȘÀÁNÀðNÀëèüçæûÌOÀðȘ
ÀÔèüüôçæûÌ£ËüÁó§ÅÅȘÀÁNÀðNÀëó§ûÌABNȘ
ÀÁ
ÀüNÀðF1NȘÀüNÀðF2NñøÝÞöˆNÀðF
1ȘNÀðF
2ÆŠüôçæûÌùª°èçá§úȘ
ÀÁ
ÀüNÀðF1N=ÎêȘÀüNÀðF2N=ÎôȘ
ÆøÀÔNF
1ȘNF
2?ó§ûÌABNȘÀÁNNÀðÀëNF
1ȘNNÀðÀëNF
2Ș
èÒNF
1=mȘNF
2=nȘå·m+n=2
ȘúØtan
Îê=Ștan
Îô=Ș
ÀÁtanÈ´Îê+ÎôÈˋ=
=
Ș
ÀÔm+n=2
Ș
ÀÁmn=mÈ´2
-mÈˋ=-È´m-
Èˋ
2+2Ș
ÆøÀÔ-5ÀÉmn-6ÀÉ-4Ș-
ÀÉÀÉ-Ș
ÀÁtanÈ´Îê+ÎôÈˋçáàÀøçñÑöÏòú[-
Ș-
]ÈÛ




 úÃúèÑÿÖøÉýãåô¢¥øÝë´û«ÅÈüçêÅÇÞ¯¡
úÃúèÑÿÖøÉýãåô¢¥øÝë´û«ÅÈüçêÅÇÞ¯¡
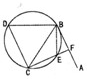 àÓë¥È˜øÝüÔABöˆåýçáúÅüÔȘúÅçÐöˆBȘçÐCåÖåýèüȘÀüABCçá§úó§ñøüÔBE§£åýÆÖEȘDBÇ¿øÝBE§£åýÆÖçÐDÈÛ
àÓë¥È˜øÝüÔABöˆåýçáúÅüÔȘúÅçÐöˆBȘçÐCåÖåýèüȘÀüABCçá§úó§ñøüÔBE§£åýÆÖEȘDBÇ¿øÝBE§£åýÆÖçÐDÈÛ