练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．设向量$\overrightarrow{AB}，\overrightarrow{CD}$分别在两条异面直线上，M，N分别为线段AC，BD的中点．求证：向量$\overrightarrow{AB}，\overrightarrow{CD}，\overrightarrow{MN}$共面．

    分析 如图所示，取AD的中点E，连接EM，EN．由三角形中位线定理可得：EN∥AB，EM∥CD，利用$\overrightarrow{EN}$，$\overrightarrow{EM}$，$\overrightarrow{MN}$共面，即可证明．

    解答 证明：如图所示，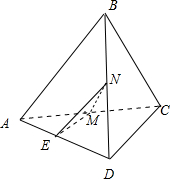
    取AD的中点E，连接EM，EN．
    由三角形中位线定理可得：
    EN∥AB，EM∥CD，
    而$\overrightarrow{EN}$，$\overrightarrow{EM}$，$\overrightarrow{MN}$共面，
    ∴向量$\overrightarrow{AB}，\overrightarrow{CD}，\overrightarrow{MN}$共面．

    点评 本题查克拉三角形中位线定理、向量共面定理，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．数列{an}为各项都是正数的等比数列，且a2，$\frac{1}{2}$a3，2a1成等差数列，则公比的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）=（x+1）2，若存在实数a，使得f（x+a）≤2x-4对任意的x∈[2，t]恒成立，则实数t的最大值为（　　）
    A．10B．8C．6D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某铝制品厂在边长为40cm的正方形铝板上割下四个半径为20厘米的圆形（如图所示的阴影部分）．该厂打算用余下的部分制作底面直径和高相等的圆柱形包装盒（接缝用料忽略不计）．问：
    （1）包装盒的最大直径是多少？（精确到0.01厘米）
    （2）画出你设计的剪裁图．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知：AB、BC、CD是不在同一平面内的三条线段，E、F、G分别为AB、BC、CD的中点．求证．AC∥平面EFG，BD∥平面EFG．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．如图所示，正方体ABCD-A1B1C1D1的棱长为1，M是AB的中点，求D1M与面ABCD所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知tan（α+$\frac{π}{4}$）=2cos2α，求α的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．在△ABC中，若b+c=$\sqrt{2}$+1，B=30°，C=45°，则（　　）
    A．b=1，c=$\sqrt{2}$B．b=$\sqrt{2}$，c=1C．b=$\frac{\sqrt{2}}{2}$，c=1+$\frac{\sqrt{2}}{2}$D．b=1+$\frac{\sqrt{2}}{2}$，c=$\frac{\sqrt{2}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．sin157°30′cos22°30′=$\frac{\sqrt{2}}{4}$．

    查看答案和解析>>

    同步练习册答案