Question

9．某铝制品厂在边长为40cm的正方形铝板上割下四个半径为20厘米的圆形（如图所示的阴影部分）．该厂打算用余下的部分制作底面直径和高相等的圆柱形包装盒（接缝用料忽略不计）．问：
（1）包装盒的最大直径是多少？（精确到0.01厘米）
（2）画出你设计的剪裁图．

Answer 1

分析 （1）以正方形的中心为原点，建立坐标系，建立直线方程和圆的方程，数形结合求出满足条件的最大直径；
（2）根据（1）中解答思路，画出满足条件的裁剪图即可．

解答 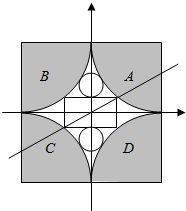解：（1）建立如图所示的直角坐标系，
若使底面直径最大，应如图所示剪裁，
设底面半径为r，由圆柱形包装盒的底面直径和高相等，
可得AD=2r，AB=2πr，则A点的坐标为：（πr，r），
直线AC的方程为：y=$\frac{1}{π}$x，…①
位于第一象限的弧所在的圆的方程为（x-20）²+（y-20）²=20²，…②，
将①代入②得：（πy-20）²+（y-20）²=20²，
解得：y≈3.01cm，或y≈12.23cm（舍去），
即r的最大值为3.01cm，
即包装盒的最大直径是6.02cm．
（2）满足条件的剪裁图如图所示：

点评 本题考查的知识点是直线与圆的位置关系，建立恰当的坐标系，将形的问题化为数的问题，是解答的关键．