
分析 先求出当x∈[0,$\frac{π}{2}$]时,sin(2x-$\frac{π}{3}$)的取值范围讨论a,建立方程关系进行求解即可.
解答 解:∵x∈[0,$\frac{π}{2}$],
∴2x∈[0,π],
2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{2π}{3}$],
则sin(2x-$\frac{π}{3}$)∈[sin(-$\frac{π}{3}$),sin$\frac{π}{2}$],
即sin(2x-$\frac{π}{3}$)∈[-$\frac{\sqrt{3}}{2}$,1],
∵当x∈[0,$\frac{π}{2}$]的最大值是1,最小值是-5,
∴若a≥0,则$\left\{\begin{array}{l}{2a+b=1}\\{-\frac{\sqrt{3}}{2}×2a+b=-5}\end{array}\right.$,得$\left\{\begin{array}{l}{2a+b=1}\\{-\sqrt{3}a+b=-5}\end{array}\right.$,得a=6(2-$\sqrt{3}$)=12-6$\sqrt{3}$,b=-23+12$\sqrt{3}$,
若a<0,则$\left\{\begin{array}{l}{2a+b=-5}\\{-\sqrt{3}a+b=1}\end{array}\right.$,得a=-6(2-$\sqrt{3}$)=6$\sqrt{3}$-12,b=25-12$\sqrt{3}$.
点评 本题主要考查三角函数最值的应用,根据条件建立方程关系是解决本题的关键.注意要对a进行分类讨论.


科目:高中数学 来源: 题型:填空题
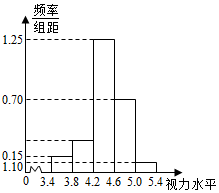 为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是6.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{4}$,0) | B. | (0,$\frac{π}{4}$) | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{π}{2}$,$\frac{3}{4}$π) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≤1 | B. | a≥1 | C. | a≤0 | D. | a≥0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com