
| A. | (-$\frac{π}{4}$,0) | B. | (0,$\frac{π}{4}$) | C. | ($\frac{π}{4}$,$\frac{π}{2}$) | D. | ($\frac{π}{2}$,$\frac{3}{4}$π) |
分析 由新定义,可得cosθ<sinθ<tanθ,可对选项一一加以判断,运用正弦函数、余弦函数和正切函数的图象和性质,即可得到结论.
解答 解:由a=tanθ,b=sinθ,c=cosθ,θ∈{θ|-$\frac{π}{4}$<θ<$\frac{3}{4}$π,θ≠0,$\frac{π}{4}$,$\frac{π}{2}$},
{a,b}max=a,{b,c}max=b,
可得cosθ<sinθ<tanθ,①
对选项A,若-$\frac{π}{4}$<θ<0,即有sinθ<0,cosθ>0,不等式①不成立;
对于选项B,若0<θ<$\frac{π}{4}$,即有sinθ<cosθ,不等式①不成立;
对于选项C,若$\frac{π}{4}$<θ<$\frac{π}{2}$,即有sinθ>cosθ,sinθ<1,tanθ>1,不等式①成立;
对于选项D,若$\frac{π}{2}$<θ<$\frac{3π}{4}$,即有sinθ>0,tanθ<0,不等式①不成立.
综上可得,选项C正确.
故选:C.
.
点评 本题考查新定义的理解和运用,考查三角函数的图象和性质,掌握正弦函数和余弦函数、正切函数的图象和性质是解题的关键


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
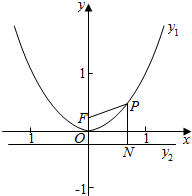 如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.
如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com