
分析 连结A1C1,B1D1,交于点O1,连结AC、BD,交于点O,以O为原点,OA为x轴,OB为y轴,OO1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AD1与B1C所成角的余弦值.
解答 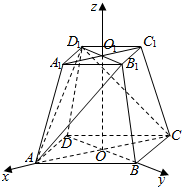 解:∵正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,
解:∵正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,
连结A1C1,B1D1,交于点O1,连结AC、BD,交于点O,
∴OB=$\frac{1}{2}BD=\frac{1}{2}\sqrt{4+4}$=$\sqrt{2}$,${O}_{1}{B}_{1}=\frac{1}{2}{B}_{1}{D}_{1}$=$\frac{1}{2}\sqrt{1+1}$=$\frac{\sqrt{2}}{2}$,
∵侧棱与底面所成的角为60°,∴BB1=2(OB-O1B1)=2($\sqrt{2}-\frac{\sqrt{2}}{2}$)=$\sqrt{2}$,
∴OO1=$\sqrt{(\sqrt{2})^{2}-(\frac{\sqrt{2}}{2})^{2}}$=$\frac{\sqrt{6}}{2}$,
以O为原点,OA为x轴,OB为y轴,OO1为z轴,建立空间直角坐标系,
A($\sqrt{2},0,0$),D1(0,-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{2}$),B1(0,$\frac{\sqrt{2}}{2},\frac{\sqrt{6}}{2}$),C(-$\sqrt{2}$,0,0),
$\overrightarrow{A{D}_{1}}$=(-$\sqrt{2}$,-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{6}}{2}$),$\overrightarrow{{B}_{1}C}$=(-$\sqrt{2}$,-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{6}}{2}$),
设异面直线AD1与B1C所成角为θ,
则cosθ=$\frac{|\overrightarrow{A{D}_{1}}•\overrightarrow{{B}_{1}C}|}{|\overrightarrow{A{D}_{1}}|•|\overrightarrow{{B}_{1}C}|}$=$\frac{|2+\frac{1}{2}-\frac{3}{2}|}{\sqrt{2+\frac{1}{2}+\frac{3}{2}}•\sqrt{2+\frac{1}{2}+\frac{3}{2}}}$=$\frac{1}{4}$.
∴异面直线AD1与B1C所成角的余弦值为$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查异面直线所成角的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
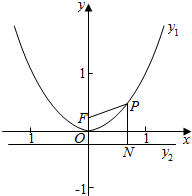 如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.
如图所示,在平面直角坐际系中有一抛物线y1=ax2,且抛物线经过点(2a-1,1),y轴上有一定点F,其坐标为(0,$\frac{1}{4}$),直线1的解析式为y2=-$\frac{1}{4}$,在抛物线上有一动点P,连接PF,并过点P作PN⊥直线1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=±1 | B. | f(x1+x2)=0 | ||
| C. | |x1+x2|的最小值为$\frac{2π}{3}$ | D. | f(x)的最小正周期为2|x1-x2| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1≤x≤2} | B. | {x|0<x≤1} | C. | {x|-1≤x≤0} | D. | {x|x≤2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com