
分析 如图所示,由正方体的性质可得:AO⊥平面BDD1.可得AC⊥BD1,可得BD1⊥平面ACB1.由EF⊥平面AB1C,可得EF∥BD1,可得EF为△ABD1的中位线,即可得出.
解答 解:如图所示.
由正方体的性质可得:AO⊥平面BDD1.
∴AC⊥BD1,
同理可得BD1⊥AB1,又AC∩AB1=A,
∴BD1⊥平面ACB1.
又EF⊥平面AB1C,
∴EF∥BD1,又点E为AD1的中点,
∴点F为AB的中点,
而$B{D}_{1}=\sqrt{3}$AB,
∴EF=$\frac{1}{2}B{D}_{1}$=$\frac{1}{2}$×$2\sqrt{3}$=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查了正方体的性质、线面垂直的判定与性质定理、三角形中位线定理,考查了推理能力与计算能力,属于中点题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2 | C. | 255 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
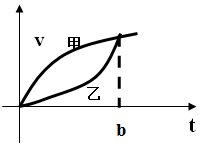 甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )
甲、乙速度v与时间t的关系如图,a(b)是t=b时的加速度,S(b)是从t=0到t=b的路程,则a甲(b)与a乙(b),S甲(b)与S乙(b)的大小关系是( )| A. | a甲(b)>a乙(b),S甲(b)>S乙(b) | B. | a甲(b)<a乙(b),S甲(b)<S乙(b) | ||
| C. | a甲(b)<a乙(b),S甲(b)>S乙(b) | D. | a甲(b)<a乙(b),S甲(b)<S乙(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 10 | C. | 17 | D. | 26 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $31\frac{15}{16}$ | B. | $32\frac{15}{16}$ | C. | $33\frac{15}{16}$ | D. | $26\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在救灾现场,搜救人员从A点出发沿正北方向行进x米到达B处,探测到一个生命迹象,然后从B处沿南偏东75°行进30米到达C处,探测到另一个生命迹象,如果C处恰好在A处的北偏东60°方向上,那么x=10$\sqrt{6}$.米.
如图,在救灾现场,搜救人员从A点出发沿正北方向行进x米到达B处,探测到一个生命迹象,然后从B处沿南偏东75°行进30米到达C处,探测到另一个生命迹象,如果C处恰好在A处的北偏东60°方向上,那么x=10$\sqrt{6}$.米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com