
【题目】某火锅店为了解气温对营业额的影响,随机记录了该店1月份中5天的日营业额y(单位:千元)与该地当日最低气温x(单位:℃)的数据,如下表:
x | 2 | 5 | 8 | 9 | 11 |
y | 12 | 10 | 8 | 8 | 7 |
(1)求y关于x的回归方程![]() ;
;
(2)判定y与x之间是正相关还是负相关;若该地1月份某天的最低气温为6℃,用所求回归方程预测该店当日的营业额;
附:①![]() ;
; .
.
②参考数据如下:
i |
|
|
|
|
1 | 2 | 12 | 4 | 24 |
2 | 5 | 10 | 25 | 50 |
3 | 8 | 8 | 64 | 64 |
4 | 9 | 8 | 81 | 72 |
5 | 11 | 7 | 121 | 77 |
| 35 | 45 | 295 | 287 |
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】某地有三家工厂,分别位于矩形ABCD的顶点A,B,及CD的中点P处,已知![]() km,
km,![]() ,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
,为了处理三家工厂的污水,现要在矩形ABCD的区域上(含边界),且A,B与等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为ykm.
(I)按下列要求写出函数关系式:
①设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
②设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式.
的函数关系式.
(Ⅱ)请你选用(I)中的一个函数关系式,确定污水处理厂的位置,使三条排水管道总长度最短.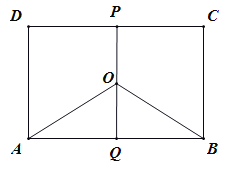
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,椭圆M:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,左右顶点分別为A,B,线段AB的长为4.P在椭圆M上且位于第一象限,过点A,B分别作l1⊥PA,l2⊥PB,直线l1,l2交于点C.
,左右顶点分別为A,B,线段AB的长为4.P在椭圆M上且位于第一象限,过点A,B分别作l1⊥PA,l2⊥PB,直线l1,l2交于点C.

(1)若点C的横坐标为﹣1,求P点的坐标;
(2)直线l1与椭圆M的另一交点为Q,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆的标准方程;
(2)若![]() ,
,![]() 为椭圆上不同的两点,且以
为椭圆上不同的两点,且以![]() 为直径的圆过坐标原点.是否存在定圆与动直线
为直径的圆过坐标原点.是否存在定圆与动直线![]() 相切?若存在,求出该圆的方程;若不存在,说明理由.
相切?若存在,求出该圆的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]:在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)判断曲线![]() ,
,![]() 是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)在平面直角坐标系xOy中,以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,l的极坐标方程为![]() ,C的参数方程为
,C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).写出l和C的普通方程;
).写出l和C的普通方程;
(2)在直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为 (t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线
(t为参数),以原点O为极点,x轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,记曲线
,记曲线![]() 和
和![]() 在第一象限内的交点为A.写出曲线
在第一象限内的交点为A.写出曲线![]() 的极坐标方程和线段OA的长.
的极坐标方程和线段OA的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为
为![]() 的中点,以
的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且二面角
的位置,且二面角![]() 为直二面角,连结
为直二面角,连结![]() .
.
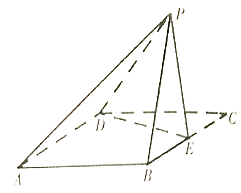
(1)记平面![]() 与平面
与平面![]() 相较于
相较于![]() ,在图中作出
,在图中作出![]() ,并说明画法;
,并说明画法;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考改革后,国家只统一考试数学和语文,英语学科改为参加等级考试,每年考两次,分别放在每个学年的上、下学期,物理、化学、生物、地理、历史、政治这六科则以该省的省会考成绩为准.考生从中选择三科成绩,参加大学相关院系的录取.
(1)若英语等级考试成绩有一次为优,即可达到某211院校的录取要求.假设某个学生参加每次等级考试事件是独立的,且该生英语等级考试成绩为优的概率都是![]() ,求该生在高二上学期的英语等级考试成绩才为优的概率;
,求该生在高二上学期的英语等级考试成绩才为优的概率;
(2)据预测,要想报考该211院校的相关院系,省会考的成绩至少在90分以上,才有可能被该校录取.假设该生在省会考六科的成绩,考到90分以上概率都是![]() ,设该生在省会考时考到90分以上的科目数为
,设该生在省会考时考到90分以上的科目数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com