
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 ,
, 是两个非零向量,则“向量
是两个非零向量,则“向量 ,
, 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x +
+ )•(
)•( -x
-x )的图象是一条开口向下的抛物线”的
)的图象是一条开口向下的抛物线”的查看答案和解析>>
科目:高中数学 来源: 题型:单选题
设a、b是两个向量,对不等式0≤|a+b|≤|a|+|b|给出下列四个结论:
①不等式左端的不等号“≤”只能在a=b=0时取等号“=”;
②不等式左端的不等号“≤”只能在a与b不共线时取不等号“<”;
③不等式右端的不等号“≤”只能在a与b均非零且同向共线时取等号“=”;
④不等式右端的不等号“≤”只能在a与b不共线时取不等号“<”.
其中正确的结论有
查看答案和解析>>
科目:高中数学 来源:东城区模拟 题型:单选题
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市东城区普通校高三(下)3月联考数学试卷(理科)(解析版) 题型:选择题
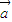 ,
,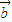 是两个非零向量,则“向量
是两个非零向量,则“向量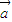 ,
,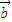 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x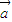 +
+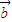 )•(
)•(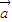 -x
-x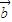 )的图象是一条开口向下的抛物线”的( )
)的图象是一条开口向下的抛物线”的( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com