
分析 (1)y=$\frac{1}{{2}^{x}+1}$,x≥0,可得$0<y≤\frac{1}{2}$.可得集合A.
(2)对于命题p:?x∈A,使得m≤x成立,可得m$≤\frac{1}{2}$.命题q:函数$f(x)=\frac{m}{x}$在(0,+∞)上单调递减,可得m>0.p∧q为假命题,p∨q为真命题,可得p与q必然一真一假.
解答 解:(1)∵y=$\frac{1}{{2}^{x}+1}$,x≥0,∴$0<y≤\frac{1}{2}$.A=$(0,\frac{1}{2}]$,
(2)对于命题p:?x∈A,使得m≤x成立,∴m$≤\frac{1}{2}$.
命题q:函数$f(x)=\frac{m}{x}$在(0,+∞)上单调递减,∴m>0.
∵p∧q为假命题,p∨q为真命题,
p与q必然一真一假.
∴$\left\{\begin{array}{l}{m≤\frac{1}{2}}\\{m≤0}\end{array}\right.$,或$\left\{\begin{array}{l}{m>\frac{1}{2}}\\{m>0}\end{array}\right.$.
解得m≤0,或$m>\frac{1}{2}$.
点评 本题考查了函数的单调性、简易逻辑的判定方法、不等式的解法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
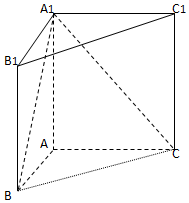 如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Y~N(aμ,σ2) | B. | Y~N(0,1) | C. | Y~N($\frac{μ}{a}$,$\frac{σ2}{b}$) | D. | Y~N(aμ+b,a2σ2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 28 | C. | 84 | D. | 96 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com